Question

A rod of length $1000{\text{mm}}$ and coefficient of linear expansion $\alpha = {10^{ - 4}}{\text{/}}^\circ {\text{C}}$ is placed on a horizontal smooth surface symmetrically between fixed walls separated by $1001{\text{mm}}$ . Young’s modulus of the rod is ${10^{11}}{\text{N}}{{\text{m}}^{ - 2}}$ . If the temperature is increased by $20^\circ {\text{C}}$ , then find the stress developed in the rod (in ${\text{N}}{{\text{m}}^{ - 2}}$ ).
A) ${10^5}$
B) ${10^8}$
C) ${10^7}$
D) ${10^6}$

Answer 1

Hint:From the given dimensions, it is clear that the rod placed between the fixed wall does not actually touch both the walls. It can be considered to touch one of the walls. Then as the temperature is increased, the rod will expand and touch the other fixed wall but it will not expand further than that, leading to the development of stress in the rod.

Formulas used:
-The change in length of a rod is given by, $\Delta l = l' - l$ where $l$ is the original length of the rod and $l$’ is the new length of the rod.
-The stress developed in a body is given by, $\sigma = Y \times \dfrac{{\Delta l}}{l}$ where $Y$ is Young’s modulus of the body and $\dfrac{{\Delta l}}{l}$ is the longitudinal strain of the body.

Complete step by step answer.
Step 1: Sketch a figure depicting the arrangement of the system under consideration and list the given parameters.

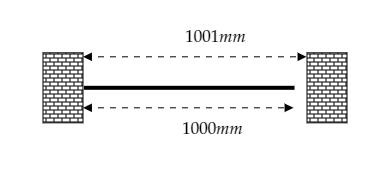
As shown in the above figure, the rod is placed horizontally between the two fixed walls such that one end of the rod is in contact with one fixed wall. When the temperature is increased, the new length of the rod will be equal to the distance between the walls.
The length of the rod is given to be $l = 1000{\text{mm}} = 1{\text{m}}$ .
The distance between the fixed walls is also the new length of the rod and it is given to be $l' = 1001{\text{mm}} = 1 \cdot 001{\text{m}}$ .
Young’s modulus of the wire is $Y = {10^{11}}{\text{N}}{{\text{m}}^{ - 2}}$ .
The coefficient of linear expansion of the rod is given to be $\alpha = {10^{ - 4}}{\text{/}}^\circ {\text{C}}$ .
Also, the change in temperature is given to be $\Delta T = 20^\circ {\text{C}}$ .
Step 2: Express the change in the length of the rod to determine the longitudinal strain of the rod.
The change in length of the rod can be expressed as $\Delta l = l' - l$ --------- (1) where $l$ is the original length of the rod and $l$’ is the new length of the rod.
Substituting for $l = 1{\text{m}}$ and $l' = 1 \cdot 001{\text{m}}$ in equation (1) we get, $\Delta l = 1 \cdot 001 - 1 = 0 \cdot 001{\text{m}}$ .
Then the longitudinal strain in the rod will be $\dfrac{{\Delta l}}{l} = \dfrac{{0 \cdot 001}}{1} = {10^{ - 3}}$
Step 3: Express the stress developed in the rod.
The stress developed in the rod is expressed as $\sigma = Y \times \dfrac{{\Delta l}}{l}$ --------- (2) where $Y$ is Young’s modulus of the rod and $\dfrac{{\Delta l}}{l}$ is the longitudinal strain of the rod.
Substituting for $Y = {10^{11}}{\text{N}}{{\text{m}}^{ - 2}}$ and $\dfrac{{\Delta l}}{l} = {10^{ - 3}}$ in equation (2) we get, $\sigma = {10^{11}} \times {10^{ - 3}} = {10^8}{\text{N}}{{\text{m}}^{ - 2}}$ .
So the stress developed is $\sigma = {10^8}{\text{N}}{{\text{m}}^{ - 2}}$ .

Thus the correct option is B.

Note:When the temperature was increased, the expansion in the rod should have been $\Delta l = l\alpha \Delta T = 1 \times {10^{ - 4}} \times 20 = 0 \cdot 002{\text{m}}$ . But because of the fixed walls on either side of the rod, the expansion of the rod is only $\Delta l = 0 \cdot 001{\text{m}}$ . It is not necessary to consider the rod to be fixed to one of the walls. Even if it was not fixed to either wall, the new length would still have been equal to the distance between the walls, though the expansion on either end of the rod may be different.