Question

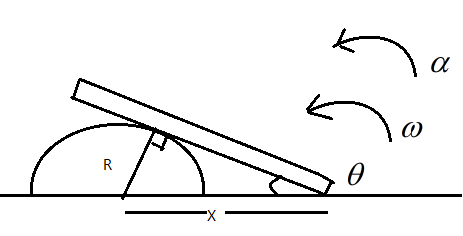
A rod leans against a stationary cylindrical body as shown in figure, and its right end slides to the right on the floor with a constant speed $v$. Choose the correct options:

\[\begin{align}
  & A.\text{ the angular speed }\omega \text{=}\dfrac{-R{{v}^{2}}(2{{x}^{2}}-{{R}^{2}})}{{{x}^{2}}{{({{x}^{2}}-{{R}^{2}})}^{\dfrac{3}{2}}}} \\
 & B.\text{ the angular acceleration }\alpha \text{=}\dfrac{Rv}{x\sqrt{{{x}^{2}}-{{R}^{2}}}} \\
 & C.the\text{angular speed }\omega \text{=}\dfrac{Rv}{x\sqrt{{{x}^{2}}-{{R}^{2}}}} \\
 & D.\text{the angular acceleration }\alpha \text{=}\dfrac{-R{{v}^{2}}(2{{x}^{2}}-{{R}^{2}})}{{{x}^{2}}{{({{x}^{2}}-{{R}^{2}})}^{\dfrac{3}{2}}}} \\
\end{align}\]

Answer 1

Hint: To begin with let us understand the definition of angular acceleration and angular velocity, first. These are often seen in bodies which undergo rotation.
We know that angular velocity $\omega$ is defined as the rate at which the angular position varies with respect to time, and also given as $\omega=\dfrac{v}{r}$ where $v$ is the linear velocity and $r$ is the from between the centre of the circle and the position of the body. Whereas, angular acceleration $\alpha$ is the change in angular velocity with respect to time.

Formula used:
 $\omega=-\dfrac{d\theta}{dt}$ and$\alpha=\dfrac{d\omega}{dt}$

Complete step-by-step answer:
Let us assume that the radius of the cylindrical body is $R$, and that the rod makes an angle $\theta$ with the ground. Let the distance between the centre of the cylinder and the point where the rod touches the ground be $X$, and let the rod move with a linear velocity $v$, angular velocity $\omega$ and experience and angular acceleration $\alpha$ as shown in the figure.

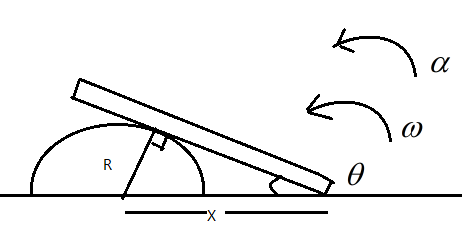
Clearly, from the diagram we can say that $sin\theta=\dfrac{R}{X}$, rearranging, we get $X=\dfrac{R}{sin\theta}$
Then we know that linear velocity of rod $v$ can be expressed as $v=\dfrac{dx}{dt}.$
Then, we have $v=\dfrac{d}{dt}\left(\dfrac{R}{sin\theta}\right)=\dfrac{-Rcos\theta\left(\dfrac{d\theta}{dt}\right)}{sin^{2}\theta}$
But we know also know that angular acceleration$\omega$ is given as $\omega=-\dfrac{d\theta}{dt}$
Then substituting the value of $\omega$in $v$, we get,
$v=\dfrac{Rcos\theta \omega }{si{{n}^{2}}\theta }$
Rearranging, we get $\omega=\dfrac{vsin^{2}\theta}{Rcos\theta}$
From $sin^{2}\theta+cos^{2}\theta=1$, we can write $cos\theta=\sqrt{1-sin^{2}\theta}$
Replacing, we get, $\omega=\dfrac{vsin^{2}\theta}{R\sqrt{1-sin^{2}\theta}}$
Substituting for $sin\theta$ as $sin\theta=\dfrac{R}{X}$, we get, $\omega=\dfrac{v\left(\dfrac{R}{X}\right)^{2}}{R\sqrt{1-\left(\dfrac{R}{X}\right)^{2}}}=\dfrac{Rv}{x\sqrt{x^{2}-R^{2}}}$
Hence we get $\omega =\dfrac{Rv}{x\sqrt{{{x}^{2}}-{{R}^{2}}}}$

We also know that angular acceleration $\alpha$ is given as$\alpha=\dfrac{d\omega}{dt}$
Then differentiating $\omega$ with respect to $t$ we get, \[\alpha =\dfrac{-Rv\left[ \sqrt{{{x}^{2}}-{{R}^{2}}}+\dfrac{x.2x}{2\sqrt{{{x}^{2}}-{{R}^{2}}}} \right]}{{{\left( x\left( \sqrt{{{x}^{2}}-{{R}^{2}}} \right) \right)}^{2}}}=\dfrac{-Rv[{{x}^{2}}-{{R}^{2}}+{{x}^{2}}]}{{{x}^{2}}{{({{x}^{2}}-{{R}^{2}})}^{\dfrac{3}{2}}}}=\dfrac{-Rv(2{{x}^{2}}-{{R}^{2}})}{{{x}^{2}}{{({{x}^{2}}-{{R}^{2}})}^{\dfrac{3}{2}}}}\]
Hence we get \[\alpha =\dfrac{-Rv(2{{x}^{2}}-{{R}^{2}})}{{{x}^{2}}{{({{x}^{2}}-{{R}^{2}})}^{\dfrac{3}{2}}}}\]
Thus the answer is
\[\begin{align}
  & C.the \text{angular speed }\omega \text{=}\dfrac{Rv}{x\sqrt{{{x}^{2}}-{{R}^{2}}}} \\
 & D.\text{the angular acceleration }\alpha \text{=}\dfrac{-R{{v}^{2}}(2{{x}^{2}}-{{R}^{2}})}{{{x}^{2}}{{({{x}^{2}}-{{R}^{2}})}^{\dfrac{3}{2}}}} \\
\end{align}\]

So, the correct answers are “Option C and D”.

Note: This question involves a lot of mathematical differentiation more than physics. You can remember the following equations for finding the derivatives, $\dfrac{d}{dt}\dfrac{u}{v}=\dfrac{vu\prime -uv\prime}{v^{2}}$, and $\dfrac{d}{dt}{uv}=vu\prime +uv\prime$ where $u\prime, v\prime$ are the first derivative of $u$, $v$ respectively.