Question

A rod is moving against a floor and a wall as shown in figure. If it’s lower end is pulled with velocity ${V_0}$ .Find out velocity of its upper end.

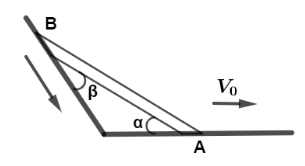
Answer 1

Hint: In order to find the magnitude of velocity of the upper end of the rod we will resolve the components of the velocity of lower end and components of the velocity of upper end and then compare these magnitudes of velocity with each other hence will find the magnitude of velocity of upper end of the rod.

Complete step by step answer:
Let us first draw the diagram, and let the net magnitude of velocity of the upper end at point $B$ is $V$ .

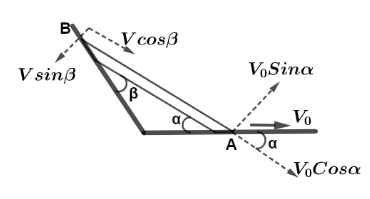
now, resolving the components of this velocity in a direction parallel to the rod and perpendicular to the rod at point B, from the diagram we can see that, two components can be written as of angle $\beta $ as
${V_\parallel } = V\cos \beta $ And ${V_ \bot } = V\sin \beta $
Now, similarly for the point A at lower end we have the components of velocity as
${V_\parallel } = {V_0}\cos \alpha $ And ${V_ \bot } = {V_0}\sin \alpha $

Now, we can see that, the parallel component of velocity of upper end and lower end is in same direction and also will be equal in magnitude in order to fall completely when it’s pulled from lower end, so equate the parallel components of velocity of both ends, we get
${V_\parallel } = {V_0}\cos \alpha $ Equals to ${V_\parallel } = V\cos \beta $ we get,
$\Rightarrow {V_0}\cos \alpha = V\cos \beta $
$\therefore V = {V_0}\dfrac{{\cos \alpha }}{{\cos \beta }}$

Hence, the velocity of the upper end of the rod will be $V = {V_0}\dfrac{{\cos \alpha }}{{\cos \beta }}$.

Note: It should be remembered that, the perpendicular components of velocity of upper end and lower end is in different direction and not having same line of action, thus this motion of slipping of rod will produce no torque, only translational motion at both ends of the rod and no rotational motion.