Questions & Answers
Question
Answers
Related Questions
A rod bent at right angle along its centre line, is placed on a rough horizontal fixed cylinder of radius R as shown in the figure. Mass of the rod is 2m and the rod is in equilibrium. Assume that the friction force on rod at A and B is equal in magnitude
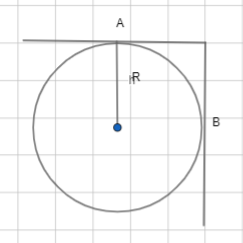
This question has multiple correct options
A. Normal force applied by cylinder on rod at A is $3mg/2$
B. Normal force applied by cylinder on rod at B must be zero
C. Friction force acting on rod at B is upward
D. Normal force applied by cylinder on rod at A is mg
Answer
![Verified]()
Verified
Verified
Hint: Draw a free body diagram according to the question and show all the components of the force. Then equate all the force components and solve the equations to find the forces which are asked in the option and compare the results to see which option is true.
Complete step by step answer:
First we will draw the component of various forces at point A and B.
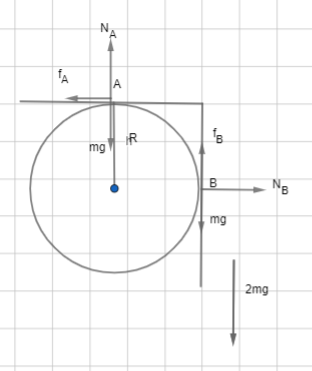
At point A we have the normal force, weight and the friction as ${{N}_{A}},mg,{{f}_{A}}$ respectively and point B we have the normal force, weight and the friction as ${{N}_{B}},mg,{{f}_{B}}$ respectively.
Now we have the total weight of the rod is 2mg. so, equating the downward weight with the upward forces we get,
\[{{N}_{A}}+{{f}_{B}}=2mg\text{ }\to \text{ 1}\]
Now comparing the horizontal forces, we get,
${{f}_{A}}={{N}_{B}}\text{ }\to \text{ 2}$
Now balancing the torque of the rod with respect to the centre, we can write,
$\begin{align}
& {{f}_{A}}R+{{f}_{B}}R=mgR \\
& {{f}_{A}}+{{f}_{B}}=mg\text{ }\to \text{ 3} \\
\end{align}$
Again, from the question we have that,
${{f}_{A}}={{f}_{B}}\text{ }\to \text{ 4}$
Now, comparing the equation 3 and equation 4, we get,
${{f}_{A}}={{f}_{B}}=\dfrac{mg}{2}$
Putting this value on equation 2, we get,
${{N}_{B}}=\dfrac{mg}{2}$
Again, from equation 1 we get,
${{N}_{A}}=\dfrac{3mg}{2}$
From these values, we can say that the normal force applied by the cylinder to the rod at point A is $\dfrac{3mg}{2}$. So, option A is true.
Normal force at point B is not zero. Option B is wrong.
Friction force on rod at point B is upward. Option C is correct.
Option D is wrong since normal force at A is $\dfrac{3mg}{2}$.
So, the correct options are (A), (C).
Note: The normal force to a body will not be always in the opposite direction to the weight of the body. The normal force will be in the opposite direction to the force the body puts on the surface it is in and is perpendicular to the surface.
Complete step by step answer:
First we will draw the component of various forces at point A and B.
At point A we have the normal force, weight and the friction as ${{N}_{A}},mg,{{f}_{A}}$ respectively and point B we have the normal force, weight and the friction as ${{N}_{B}},mg,{{f}_{B}}$ respectively.
Now we have the total weight of the rod is 2mg. so, equating the downward weight with the upward forces we get,
\[{{N}_{A}}+{{f}_{B}}=2mg\text{ }\to \text{ 1}\]
Now comparing the horizontal forces, we get,
${{f}_{A}}={{N}_{B}}\text{ }\to \text{ 2}$
Now balancing the torque of the rod with respect to the centre, we can write,
$\begin{align}
& {{f}_{A}}R+{{f}_{B}}R=mgR \\
& {{f}_{A}}+{{f}_{B}}=mg\text{ }\to \text{ 3} \\
\end{align}$
Again, from the question we have that,
${{f}_{A}}={{f}_{B}}\text{ }\to \text{ 4}$
Now, comparing the equation 3 and equation 4, we get,
${{f}_{A}}={{f}_{B}}=\dfrac{mg}{2}$
Putting this value on equation 2, we get,
${{N}_{B}}=\dfrac{mg}{2}$
Again, from equation 1 we get,
${{N}_{A}}=\dfrac{3mg}{2}$
From these values, we can say that the normal force applied by the cylinder to the rod at point A is $\dfrac{3mg}{2}$. So, option A is true.
Normal force at point B is not zero. Option B is wrong.
Friction force on rod at point B is upward. Option C is correct.
Option D is wrong since normal force at A is $\dfrac{3mg}{2}$.
So, the correct options are (A), (C).
Note: The normal force to a body will not be always in the opposite direction to the weight of the body. The normal force will be in the opposite direction to the force the body puts on the surface it is in and is perpendicular to the surface.
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
-
LIVECourses
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
