Question

A rocket of height h meters is fired vertically upwards. Its velocity at time t seconds is (2t + 3 ) meters per second. If the angle of elevation of the top of the rocket from a point on the ground after 1 second of firing is $\dfrac{\pi }{6}$ and after 3 seconds it is $\dfrac{\pi }{3}$then the distance at the point from the rocket is
A) $14\sqrt 3 meters$
B) $7\sqrt 3 meters$
C) $2\sqrt 3 meters$
D) Cannot be found without the value of h.

Answer 1

Hint:
By integrating the given velocity we get the displacement and substituting the values of t we get the values of BC and BD and using the given angle of elevation we can find the distance at the point from which the rocket is projected.

Complete step by step solution:

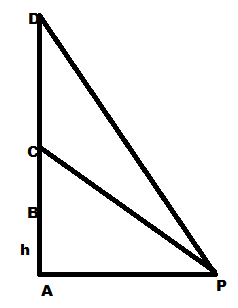
We are given that the velocity of the rocket is (2t + 3 ) meters per second
$ \Rightarrow \dfrac{{dx}}{{dt}} = 2t + 3$
Now to find the displacement x we need to integrate the velocity
$
   \Rightarrow dx = \left( {2t + 3} \right)dt \\
   \Rightarrow \int {dx = \int {\left( {2t + 3} \right)dt} } \\
   \Rightarrow x = \dfrac{{2{t^2}}}{2} + 3t + c = {t^2} + 3t + c \\
 $
Now we have the displacement
The displacement BC is made when t = 1
$ \Rightarrow BC = {1^2} + 3(1) + c = 4 + c$
The displacement BD is made when t = 3
$ \Rightarrow BD = {3^2} + 3(3) + c = 18 + c$
Now at t = 1 the angle of elevation is $\dfrac{\pi }{6}$
Therefore $\tan \dfrac{\pi }{6} = \dfrac{{h + 4 + c}}{{AP}}$ …………(1)
Now at t = 3 the angle of elevation is $\dfrac{\pi }{3}$
Therefore $\tan \dfrac{\pi }{3} = \dfrac{{h + 18 + c}}{{AP}}$ …………..(2)
Subtracting (2) – (1)
$
   \Rightarrow \tan \dfrac{\pi }{3} - \tan \dfrac{\pi }{6} = \dfrac{{h + 18 + c - h - 4 - c}}{{AP}} \\
   \Rightarrow \sqrt 3 - \dfrac{1}{{\sqrt 3 }} = \dfrac{{14}}{{AP}} \\
   \Rightarrow \dfrac{2}{{\sqrt 3 }} = \dfrac{{14}}{{AP}} \\
   \Rightarrow AP = 14 \times \dfrac{{\sqrt 3 }}{2} = 7\sqrt 3 meters \\
 $

Hence we get the distance of the rocket to be $7\sqrt 3 meters$. The correct option is (B).

Note:
Height is the measurement of an object in the vertical direction and distance is the measurement of an object from a particular point in the horizontal direction.
So if we know the height of the object and the linear distance, we can easily find out the angle by trigonometric formula. It is given by tan = Height / distance . The angle of elevation of the sun that is better known as altitude angle, can also be found by the same method.