Question

A rocket is in the form of a circular cylinder closed at the lower end with a cone of the same radius attached to the top. The cylinder is of radius $2.5m$ and height $21m$ and the cone has the slant height $8m$. Calculate the volume of the rocket.

Answer 1

Hint: It is given that the rocket is in the form of a cylinder. It is closed at one end and a cone is attached to the top of it. Therefore, we need to combine both the cylinder and the cone to find out the volume. We can find the volume of the cylinder and cone separately and then add them to get the final answer.
Formulas used for solving are:
Volume of Cylinder, ${V_{cy}} = \pi {r^2}h$
Volume of Cone, ${V_{co}} = \dfrac{1}{3}\pi {r^2}h$
Where, $r$ is the radius of the cylinder and the cone
$h$ is the height of the cylinder and the cone
${h_1}$ is the slant height of the cone

Complete step-by-step answer:
We can draw the given question as below:

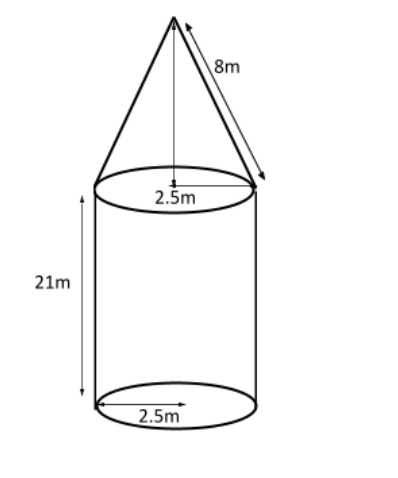
From the above figure, we need to calculate the height of the cone,
Using Pythagoras Theorem, we have,
${8^2} = {h^2} + {2.5^2}$
Shifting the terms and taking square roots on both sides of the equation, we get,
$\eqalign{
  & h = \sqrt {64 - 6.25} \cr
  & h = \sqrt {57.75} \cr
  & h = 7.6m \cr} $
Let us first consider the cylinder and find the volume of the cylinder.
From the above formula, we have,
${V_{cy}} = \pi {r^2}h$
The values of $r,h$ are given.
$\eqalign{
  & \Rightarrow {V_{cy}} = \pi \times {2.5^2} \times 21 \cr
  & \Rightarrow {V_{cy}} = 3.14 \times 131.25 \cr
  & \Rightarrow {V_{cy}} = 412.13{m^3} \cr} $
Now, let us move on to the cone.
We need to use the height which we calculated above.
$\eqalign{
  & \Rightarrow {V_{co}} = \dfrac{1}{3}\pi \times {2.5^2} \times 7.6 \cr
  & \Rightarrow {V_{co}} = \dfrac{1}{3} \times 3.14 \times 47.5 \cr
  & \Rightarrow {V_{co}} = 49.72{m^3} \cr} $
Now, adding these will give the volume of the rocket
$\eqalign{
  & V = {V_{cy}} + {V_{co}} \cr
  & V = 412.13 + 49.72 \cr
  & V = 461.8{m^3} \cr
  & V \simeq 462{m^3} \cr} $
Therefore, the final answer is $462{m^3}$
So, the correct answer is “Option B”.

Note: Make sure that all the values are given in meters or centimeters. Convert if necessary. Note that the slant height of the cone is given, do not substitute that as the height for calculating the volume of the cone. Volume is expressed in cubic meters, do not forget to write the units.