Question

A rocket fired from the earth to the moon. The distance between the earth and the moon is r and the mass of the earth is 81 times the mass of the moon. The gravitational force on the rocket will be zero, when its distance from the moon is then:
A) $\dfrac{r}{{20}}$.
B) $\dfrac{r}{{15}}$.
C) $\dfrac{r}{{10}}$
D) $\dfrac{r}{5}$

Answer 1

Hint:The gravitational force on anybody depends on the mass of the planet which is exerting force on the body also the distance from the centre of the planet and the universal gravitational constant also the gravitational force on the body can be different for different planets exerting gravitational force on the body.

Formula used:The formula of the gravitational force is given by,
$F = G\dfrac{{M \cdot m}}{{{d^2}}}$
Where the universal gravitational constant is G the masses of different objects is M and m also the distance between the centre of the two bodies is d.

Complete step by step answer:
It is given in the problem that a rocket fired from the earth to the moon. The distance between the earth and the moon is r and the mass of the earth is 81 times the mass of the moon and we need to find the distance at which the rocket will experience zero force.
Let the point at which the rocket will experience zero force is P and which is x distance from the moon therefore the distance from the earth will be r-x.

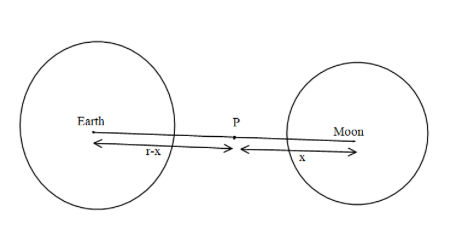
The formula of the gravitational force is given by,
$F = G\dfrac{{M \cdot m}}{{{d^2}}}$
Where the universal gravitational constant is G the masses of different objects is M and m also the distance between the centre of the two bodies is d.
The gravitational force on the rocket due to earth is equal to,
$ \Rightarrow {F_e} = G\dfrac{{{M_e} \cdot {m_r}}}{{{{\left( {r - x} \right)}^2}}}$………eq. (1)
The gravitational force on the rocket due to moon is equal to,
$ \Rightarrow {F_m} = G\dfrac{{{M_m} \cdot {m_r}}}{{{{\left( x \right)}^2}}}$………eq. (2)
As the force on the point P is equal therefore equating equation (1) and equation (2).
$ \Rightarrow {F_e} = {F_m}$
$ \Rightarrow G\dfrac{{{M_e} \cdot {m_r}}}{{{{\left( {r - x} \right)}^2}}} = G\dfrac{{{M_m} \cdot {m_r}}}{{{{\left( x \right)}^2}}}$
$ \Rightarrow \dfrac{{{M_e}}}{{{{\left( {r - x} \right)}^2}}} = \dfrac{{{M_m}}}{{{{\left( x \right)}^2}}}$
Since mass of earth is 81 times mass of moon therefore,
\[ \Rightarrow \dfrac{{81 \cdot {M_m}}}{{{{\left( {r - x} \right)}^2}}} = \dfrac{{{M_m}}}{{{{\left( x \right)}^2}}}\]
$ \Rightarrow \dfrac{{81}}{{{{\left( {r - x} \right)}^2}}} = \dfrac{1}{{{{\left( x \right)}^2}}}$
$ \Rightarrow 81 \cdot {\left( x \right)^2} = {\left( {r - x} \right)^2}$
$ \Rightarrow 81 = \dfrac{{{{\left( {r - x} \right)}^2}}}{{{{\left( x \right)}^2}}}$
Taking square root,
$ \Rightarrow 9 = \dfrac{{r - x}}{x}$
$ \Rightarrow 9x = r - x$
$ \Rightarrow 10x = r$
$ \Rightarrow x = \dfrac{r}{{10}}$
The distance from the moon at which the rocket has zero gravitational force is equal to $x = \dfrac{r}{{10}}$. The correct option for this problem is option C.

Note:The gravitational force for two different planets is always different but there can be a point between two planets exerting gravitational force on the same body where the force is equal also the body will experience zero force as the force exerted by two planets are equal and opposite.