Question

A river is flowing towards with a velocity of $ 5m/s $ . The boat velocity is $ 10m/s $ . The boat crosses the river by the shortest path. Hence,
 $ \left( A \right) $ The direction of the boat's velocity is $ 30{}^\circ $ west of north.
 $ \left( B \right) $ The direction of the boat's velocity is north west.
 $ \left( C \right) $ Resultant velocity is $ 5\sqrt{3}m/s $
 $ \left( D \right) $ Resultant velocity of boat is $ 5\sqrt{2}m/s $

Answer 1

Hint :To solve this question, we have to know about velocity and also about the angles. Velocity is characterized as the rate change of uprooting per unit time. Speed in a particular way is otherwise called speed. Velocity is equivalent to uprooting separated by time. And, tan theta is we can say, is the proportion of the contrary side to the adjacent side.

Complete Step By Step Answer:
According to the question, we can say that the angle $ \theta $ (say) is in the west or north. And, we can say, $ \tan \theta =\frac{5}{10}=0.5 $ so $ \theta ={{\tan }^{-1}}0.5 $ $ \therefore \theta =26.56505118{}^\circ $ (according to the diagram)
Here, $ 5m/s $ is the velocity of the river and $ 10m/s $ is the velocity of the boat.
Which means the theta, $ \theta $ is equal to $ 26.56505118{}^\circ $ .

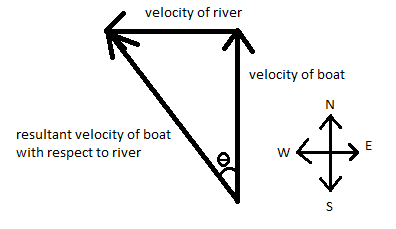
Now, we are considering, the resultant velocity is equal to $ {{V}_{r}} $
According to the formula, $ {{V}_{r}}=\sqrt{{{\left( 10 \right)}^{2}}-{{\left( 5 \right)}^{2}}}=5\sqrt{3}m/s $ (after putting the values of the velocities given in the question)
That means the options $ \left( B \right) $ and $ \left( C \right) $ both are correct.

Note :
We have to keep in our mind that, here, because we had the velocity of the boat and the velocity of the river that is why we calculated the tan theta part according to the diagram and the definition of the tan theta. Otherwise we cannot be able to do the calculation correctly.