Question

A river flows due south with a speed of $2{\text{m}}{{\text{s}}^{ - 1}}$. A man steers a motorboat across the river due east. His velocity relative to the water is ${\text{4m}}{{\text{s}}^{ - 1}}$. The river is ${\text{800m}}$ wide. Then find
A) his velocity (magnitude and direction) relative to the earth.
B) the time required to cross the river.
C) how far south of his starting point he reaches the opposite bank.

Answer 1

Hint:The man steering the boat in a moving river can be viewed as the motion of a body in a moving frame of reference. As the man steers the motorboat across the river the current of the river will drift the boat to some distance along the south. A graph representing the east direction along the positive x-direction and south along the negative y-direction will help to visualize the problem better.

Formula used:
-The absolute velocity of a body in a moving frame of reference is given by, ${\vec v_b} = {\vec v_{b/fr}} + {\vec v_{fr}}$ where ${\vec v_{b/fr}}$ is the relative velocity of the body and ${\vec v_{fr}}$ is the velocity of the frame of reference.
-The time taken to cover a displacement $d$ is given by, $t = \dfrac{d}{v}$ where $v$ is the velocity of the body.

Complete step by step answer.
Step 1: Sketch a graph representing the east and south directions to represent the velocities involved and list the parameters known from the question.

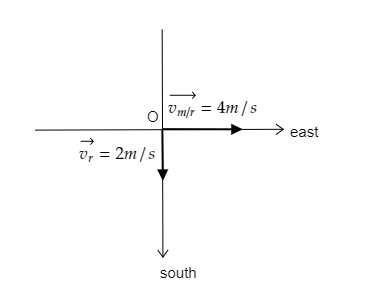
In the above figure, the velocity of the man relative to the river due east is represented along the positive x-direction ${\vec v_{m/r}} = {\text{4m}}{{\text{s}}^{ - 1}}$ and the velocity of the river due south is given is represented along the negative y-direction ${\vec v_r} = 2{\text{m}}{{\text{s}}^{ - 1}}$ .
The width of the river refers to the displacement of the man i.e., $d = 800{\text{m}}$ .
Step 2: Draw the resultant vector of ${\vec v_{m/r}} = {\text{4m}}{{\text{s}}^{ - 1}}$ and ${\vec v_r} = 2{\text{m}}{{\text{s}}^{ - 1}}$ to find the velocity of the man with respect to earth.
The velocity of the man relative to the earth is expressed as ${\vec v_m} = {\vec v_{m/r}} + {\vec v_r}$
Then the resultant velocity ${\vec v_m}$ will be the diagonal of the parallelogram formed by the vectors ${\vec v_{m/r}}$ and ${\vec v_r}$. The below figure represents this.

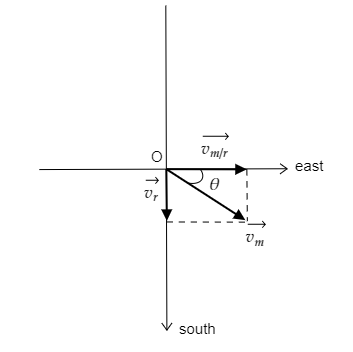
By Pythagoras theorem, the magnitude of the velocity of man relative to the earth can be obtained as ${v_m} = \sqrt {v_{m/r}^2 + v_r^2} $
Substituting values for ${v_{m/r}} = {\text{4m}}{{\text{s}}^{ - 1}}$ and ${v_r} = 2{\text{m}}{{\text{s}}^{ - 1}}$ in the above equation we get, ${v_m} = \sqrt {{4^2} + {2^2}} = \sqrt {20} {\text{m}}{{\text{s}}^{ - 1}}$ or ${v_m} = 2\sqrt 5 {\text{m}}{{\text{s}}^{ - 1}}$
The magnitude of the velocity of the man relative to the earth is ${v_m} = 2\sqrt 5 {\text{m}}{{\text{s}}^{ - 1}}$ .
From the above figure, we have $\tan \theta = \dfrac{{{{\vec v}_r}}}{{{{\vec v}_{m/r}}}} = \dfrac{2}{4} = \dfrac{1}{2}$
The direction of the velocity of the man relative to the earth will be $\theta = {\tan ^{ - 1}}\left( {\dfrac{1}{2}} \right)$ .
Step 3: Express the relation for the time taken to cross the river.
The displacement of the man as he crosses the river is $d = 800{\text{m}}$ and his velocity in doing so is ${v_{m/r}} = {\text{4m}}{{\text{s}}^{ - 1}}$ .
Then the time taken to cross the river is given by, $t = \dfrac{d}{v}$
On substituting for $d = 800{\text{m}}$ and ${v_{m/r}} = {\text{4m}}{{\text{s}}^{ - 1}}$ we get, $t = \dfrac{{800}}{4} = 200{\text{s}}$
The time taken to cross the river is $t = 200{\text{s}}$ .
Step 4: Sketch an appropriate graph and find the drift of the boat as it reaches the opposite bank.

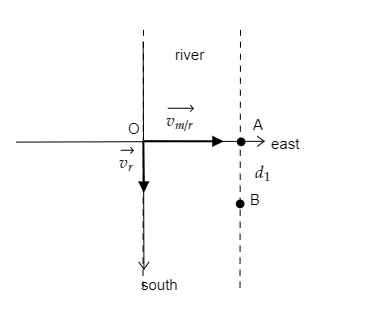
In the above figure, O represents the starting point of the man. As the man steers the boat to cross the river, his position should be at A. But the current of the river causes the boat to drift to point B. The distance between the points A and B will represent how far from the man’s starting point he reaches the opposite bank.
The distance of drift ${d_1}$ will be the product of the time taken to cross the river and the velocity of the river.
i.e., ${d_1} = t \times {v_r}$
Substituting values for $t = 200{\text{s}}$ and ${v_r} = 2{\text{m}}{{\text{s}}^{ - 1}}$ in the above expression we get, ${d_1} = 200 \times 2 = 400{\text{m}}$
The man reaches the opposite bank at a distance ${d_1} = 400{\text{m}}$ due south from his initial position.

Note: Here, the frame of reference is the river and it is moving. While calculating the time taken to cross the river, the velocity of the man relative to the river is taken because his frame of reference is not stationary and so relative velocity must be used. Also, while calculating the distance of drift, we use the velocity of the river because it is the current of the river that causes the drift.