Question

A river $4.0$ miles wide is flowing at the rate of $2\,miles/hr$. The minimum time taken by a boat to cross the river with a speed $V=4\,miles/hr$ (in still water) is approximately

A. 1 hour and 9 minutes

B. 2 hours and 7 minutes

C. 1 hour and 12 minutes

D. 2 hours and 25 minutes

Answer 1

Hint: In this question we have to apply the concept of relative velocity and vectors. We have to find the velocity of the boat and then we have to find the time taken by the boat to cross the river.

Complete step by step answer:

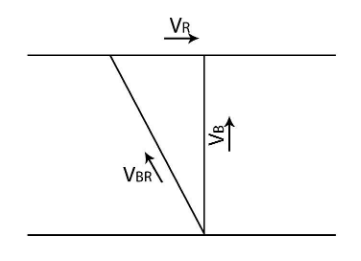
If we picturise the scenario in the question, we can see the velocities of the boat, the river and the boat with respect to the river, if the time taken by the boat to cross the river is minimum then the velocity of the boat is perpendicular to the flow of the river, then the velocity of boat with respect to the river is at some angle opposite to the flow of river,  the diagram is as follows:

Where, ${V_R}$ is the velocity of river, ${V_B}$ is the velocity of the boat and ${V_{BR}}$ is the velocity of the boat with respect to the river.The above set of velocities can be considered as vectors and we have to find the value of ${V_B}$.We will use the triangle laws of Vectors to find the value.Using Triangle law, we get 

${({V_B})^2} = {({V_{BR}})^2} - {({V_R})^2}$

$\Rightarrow({V_B}) = \sqrt {{{({V_{BR}})}^2} - {{({V_R})}^2}} $

Now we will put the values in this equation which are given in the question,

$({V_B}) = \sqrt {{{(4)}^2} - {{(2)}^2}} $

$\Rightarrow({V_B}) = \sqrt {16 - 4} $

$\Rightarrow({V_B}) = \sqrt {12} $

$\Rightarrow({V_B}) = \sqrt {12} $

$\Rightarrow ({V_B}) = 2\sqrt 3 $

Therefore, the velocity of the boat is $2\sqrt 3 $ miles/hour.

Now that we have the velocity of boat, we should calculate the time taken by it to cross the width of the river, the time taken by the boat is given by:

${\rm{Time}}\,{\rm{ = }}\,\,\dfrac{{{\rm{distance}}}}{{{\rm{velocity}}}}$.

We have a river width of 4miles and that is the distance the boat has to cover and the velocity is the value we have calculated above.Putting all those values we get,

Time = $\dfrac{4}{{2\sqrt 3 }}$

$ \therefore Time =\dfrac{2}{{\sqrt 3 }}$

Which is 1.154 hours, and when converted it is 1 hour and 9 minutes. 

Therefore, the correct option is (A).

Note:  The students should take care about the direction of the vectors properly and while applying the triangle law appropriate sign convention should be used. Proper distinction between velocity of boat and velocity of boat with respect to river should be done.