Question

A river 3m deep and 40m wide is flowing at the rate of 2Km per hour. How much water will fall into the sea in a minute?

Answer 1

Hint: We look at the river as a cuboid whose length will be given by the speed of water flowing per hour. Use the conversion of kilometers into meters and hours into minutes. Using a unitary method find the length to which the water flows in one minute. Use the formula for volume of a cuboid to find the volume of water that falls into the sea in 1 minute.
* Unitary method helps us to find the value of a single unit if we are given the value of multiple units and the number of units by dividing the value of multiple units by the number of units.
* Volume of a cuboid having length ‘l’, breadth ‘b’ and height ‘h’ is given by \[l \times b \times h\]
* 1Kilometers has 1000 meters
* 1 hour has 60 minutes

Complete step-by-step answer:
We can draw a diagram of the situation by showing a section of the river.

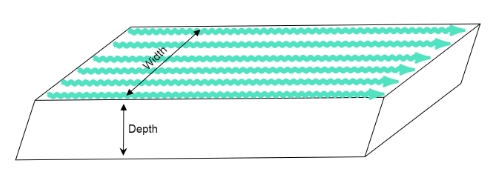
We are given that the rate of flow of water in the river is 2Km per hour
\[ \Rightarrow \]Length to which water flows in 1 hour \[ = 2\]Km
We know 1 hour has 60 minutes, so we can write
\[ \Rightarrow \]Length to which water flows in 60 minutes \[ = 2\]Km
We know 1 kilometers has 1000 meters, so we can write
\[ \Rightarrow \]Length to which water flows in 60 minutes \[ = 2 \times 1000\]m
\[ \Rightarrow \]Length to which water flows in 60 minutes \[ = 2000\]m
Now we can find the length to which water flows in 1 minute using unitary method. Divide the length to which water flows in 60 minutes by 60
\[ \Rightarrow \]Length to which water flows in 1 minute \[ = \dfrac{{2000}}{{60}}\]m
Now cancel all common factors between numerator and denominator of the term
\[ \Rightarrow \]Length to which water flows in 1 minute \[ = \dfrac{{100}}{3}\]m
\[ \Rightarrow l = \dfrac{{100}}{3}\]m
We are given the river is 3 meter deep, so the height of the river is 3m.
\[ \Rightarrow h = 3\]m
Also, the river is 40m wide, so the breadth of the river is 40m.
\[ \Rightarrow b = 40\]m
Then we can find volume of water that falls into the sea in 1 minute
Volume \[ = l \times b \times h\]
Substitute the values of length, breadth and height
\[ \Rightarrow \]Volume \[ = \dfrac{{100}}{3} \times 40 \times 3\]
Cancel the same factors from numerator and denominator.
\[ \Rightarrow \]Volume \[ = 100 \times 40\]
\[ \Rightarrow \]Volume \[ = 4000\]\[{m^3}\]

So, the amount of water falling into the sea in 1 minute is 4000\[{m^3}\]

Note: Alternate method:
We can find the area of the river by given dimensions
Height of the river is 3m
Width of the river is 40m
So, Area of the river is height multiplied by width
\[ \Rightarrow \]Area of river\[ = 3 \times 40\]
\[ \Rightarrow \]Area of the river\[ = 120\]\[{m^2}\]
Now we know rate of flow of water is 2Km per hour
We can find the amount of water falling in the river by multiplying the area of the river by the flow rate.
\[ \Rightarrow \]Amount of water falling in the sea in 1 hour \[ = 120\]\[{m^2}\]\[ \times \]2Km
Convert the value in Km using conversion 1Km \[ = \]1000m and convert the time in hours using conversion 1hour \[ = \]60 minutes
\[ \Rightarrow \]Amount of water falling in the sea in 60 minutes \[ = 120 \times 2 \times 1000\]\[{m^2}\]
\[ \Rightarrow \]Amount of water falling in the sea in 60 minutes \[ = 240000\]\[{m^2}\]
Use unitary method to find the amount of water falling in the sea in 1 minute
\[ \Rightarrow \]Amount of water falling in the sea in 1 minute \[ = \dfrac{{240000}}{{60}}\]\[{m^2}\]
\[ \Rightarrow \]Amount of water falling in the sea in 1 minute \[ = 4000\]\[{m^2}\]