Question

A ring of radius R rolls on a horizontal ground with linear speed $v$ angular speed $\omega$ what is the value of $\theta$ the velocity of point P is in vertical direction. $(v

Answer 1

Hint: We know that linear speed is the measure at which the object travels or covers a certain linear distance. And angular speed is the measure at which a rotating object covers a certain circular path. Using the two and their relationship, we can solve the following question as shown below.

Complete step-by-step solution:
A body which undergoes rotation like the seconds hand here has two kinds of velocity namely the angular velocity$\omega$ and the linear velocity$v$ .The linear velocity is mathematically defined as $v=\dfrac{s}{t}$ where $s$ is the linear distance covered in time $t$ whereas angular velocity is mathematically defined as $\omega=\dfrac{\theta}{t}$ where $\theta$ is the angular distance covered at time $t$ . Also the relationship between the two is given as $v=\omega R$, where $R$ is the radius of the circular path
Since $s=R\theta$ or the length of the arc $s$ is the product of the radius $R$ and the angle $\theta$ subtended by it in the circle, as shown in the figure below

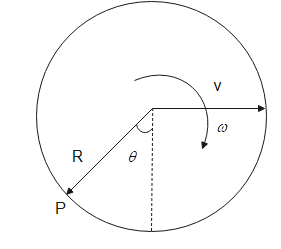
Hence solving the above equations, we get$v=\omega R$
Clearly at point P there is the net velocity is the sum of angular and linear velocity, and is written as$V_p=\omega r+v$. Consider the axis as shown below.

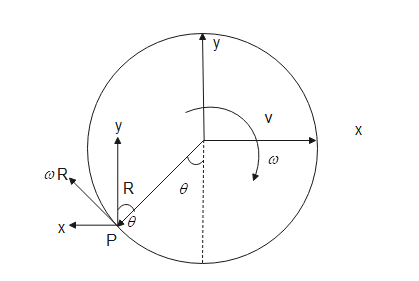
Then resolving the components we have, $V_p=\omega R sin\theta \hat j-\omega R cos\theta \hat i+v\hat i$
$\implies V_p=\omega R sin\theta \hat j+(-\omega R cos\theta +v)\hat i$
Since the velocity of point P is in vertical direction, we have
$\implies V_p=(-\omega R cos\theta +v)\hat i=0$
$\implies \omega R cos\theta =v$
$\implies \theta =cos^{-1}\dfrac{v}{\omega R}$
Thus the value of $\theta$ is $cos^{-1}\dfrac{v}{\omega R}$

Note:Linear velocity helps in the movement of the object in the forward direction, whereas the angular velocity is due to the centripetal force acting on the rotating object and helps in the tangential direction; hence both are required for the rotating object to be stable.