Question

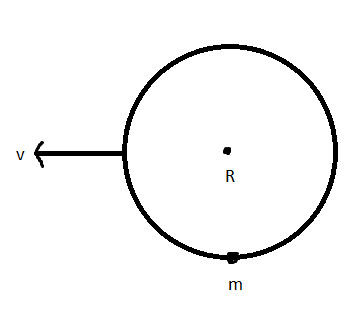
A ring of radius R lies in the vertical plane. A bead of mass ‘m’ can move along the ring without friction. Initially, the bead is at rest at the bottom-most point on the ring. Find the minimum constant horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.

Answer 1

Hint: This problem can be solved easily in the frame of reference moving along with the ring with a velocity v. In this frame the bead will have a relative velocity v in the opposite direction (towards the right). Thus, in this frame the bead has kinetic energy. This kinetic energy gets converted into potential energy when the bead reaches the top and allows it to eventually complete the full circle.

Formula used:
$\text{Kinetic Energy of a particle }\left( KE \right)\text{ = }\dfrac{1}{2}m\times {{v}^{2}}$
Where m is the mass of the particle, v is its velocity.
$\text{Potential Energy of a particle }\left( PE \right)=mgh$
Where g is the acceleration due to gravity, and h is the height of the particle from a reference point.
$\text{Decrease in Kinetic Energy = Increase in potential energy}$

Complete step by step answer:
As explained in the hint, in the frame of reference moving along with the ring, the bead will have an opposite velocity $v$.
Therefore, let us proceed as explained in the hint.
Now,
$\text{Kinetic Energy of a particle }\left( KE \right)\text{ = }\dfrac{1}{2}m\times {{v}^{2}}$ --(1)
where m is the mass of the particle, v is its velocity.
$\text{Potential Energy of a particle }\left( PE \right)=mgh$
Where g is the acceleration due to gravity, and h is the height of the particle from a reference point.

Using (1)
Initial kinetic energy of the bead = $\dfrac{1}{2}m{{v}^{2}}$
Now, for the bead to complete a full circle, velocity of the bead at the top must be greater than or equal to zero.
 For the minimum velocity required to complete the full circle, velocity of the bead at the top must be zero.

Therefore, final kinetic energy = 0.
Therefore, decrease in kinetic energy in kinetic energy = $\dfrac{1}{2}m{{v}^{2}}-0=\dfrac{1}{2}m{{v}^{2}}$
Using (2) and considering the bottom of the ring as the reference point.
Initial potential energy = 0.
Now, the vertical distance of the top from the bottom of the ring is its diameter that is twice its radius.
So, $h=2R$
Therefore, final potential energy = $mgh=2mgR$
Therefore, increase in potential energy = $2mgR-0=2mgR$
Now, since the total mechanical energy of a body remains conserved when acted upon by a conservative force (like gravity),
$\text{Decrease in Kinetic Energy = Increase in potential energy}$
$\therefore \dfrac{1}{2}m{{v}^{2}}=2mgR$
$\therefore {{v}^{2}}=4gR$
$\therefore v=\sqrt{4gR}$
Therefore, the minimum horizontal velocity required will be$\sqrt{4gR}$.

Note: Many problems like these can be easily solved by the change of frame of reference from the inertial frame. It is a good method to solve such questions but while doing so it is imperative that all respective relative velocities and pseudo forces are correctly assigned.
The total mechanical energy is only conserved when acted upon by a conservative force like gravity. In case of dissipative non-conservative forces like friction the total mechanical energy is not conserved. Then the total energy is conserved. The question mentioned frictionless rings. If the question mentioned that the ring had friction then it would have been a different case altogether.