Question

A ring cut with an inner radius 4.85cm and outer radius 4.95cm is supported horizontally from one of the pans of a balance so that it comes in contact with the water in a vessel. If surface tension of water is $70\times {{10}^{-3}}N{{m}^{-1}}$, then the extra mass in the other pan required to pull the ring away from water is
(A) 2g
(B) 3g
(C) 4.4g
(D) 15g
(E) 10g

Answer 1

Hint: Consider the force acting due to surface tension. To pull the ring away from water we need extra force to balance the force due to surface tension. First list down all the given quantities and apply the correct formula to calculate the unknown quantity.

Complete step-by-step solution -

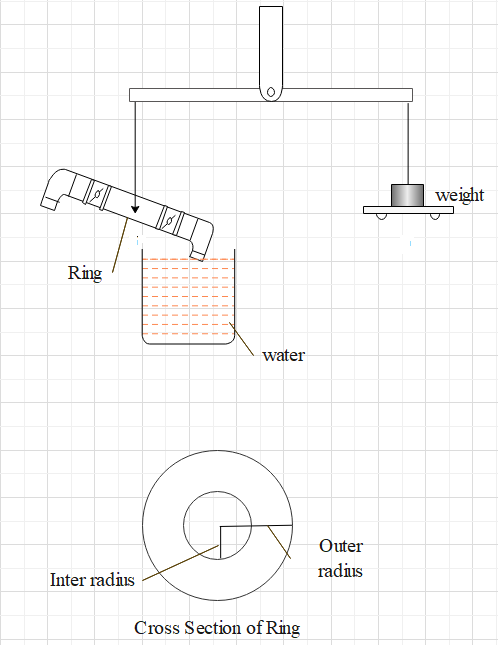
Given that
Inner radius = ${{r}_{1}}=4.85cm$
Outer radius = ${{r}_{2}}=4.95cm$
Surface tension = $T=70\times {{10}^{-3}}N{{m}^{-1}}$
We know that force due to surface tension is given by
\[\begin{align}
  & {{F}_{T}}=2\pi T({{r}_{1}}+{{r}_{2}}) \\
 & {{F}_{T}}=2\times 3.142\times 70\times {{10}^{-3}}\times (4.85+4.95)\times {{10}^{-2}} \\
 & {{F}_{T}}=4.31\times {{10}^{-2}}N \\
\end{align}\]
Extra mass required to balance this force due to surface tension is given by
$mg={{F}_{T}}$
Where g is acceleration due to gravity.
Thus,
$\begin{align}
  & m=\dfrac{{{F}_{T}}}{g} \\
 & m=\dfrac{4.31\times {{10}^{-2}}}{9.8} \\
 & m=4.4\times {{10}^{-3}}kg \\
 & m=4.4g \\
\end{align}$
Therefore, the extra mass required to pull the ring away from water is 4.4g
Hence, option (C).is correct.

Additional Information:
The imbalance of attractive molecular forces on the surface of liquid gives rise to surface tension. This surface tension is responsible for rise or fall of liquid in capillaries. The water transport from roots to leaves in plants is possible due this surface tension.

Note: Take care that all the units used are in the same system of units. Be careful while converting units from one system to another. Remember all fundamental units so that it will be easy to convert derived units from one system to another.