Question

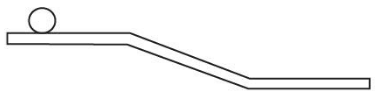
A rigid roll without slipping on a surface shows below.

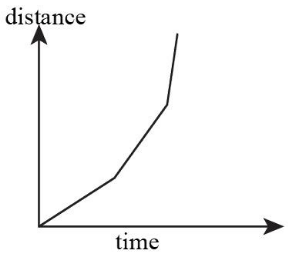
A.

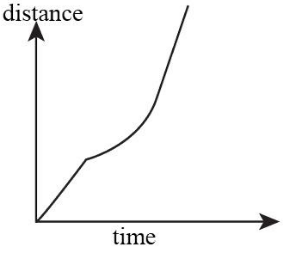
B.

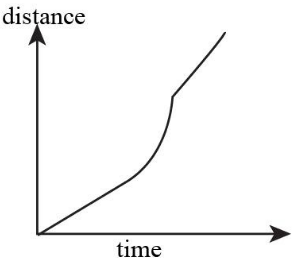
C.

D.

Answer 1

Hint: The above problem can be resolved using linear motion concepts and the mathematical equations associated with the linear motion, along with each significant variable. We are given a graph for which we need to obtain the correct selection of a distance-time graph. After the analysis, the result is determined.

Complete step by step answer:
From the given figure we can conclude that the magnitude of acceleration of ball while moving the upper horizontal part is zero and the expression for the distance is,
\[d = v \times t\]
Here, d is distance, v is speed and t is time.
Now, for the inclined part, we can observe that while moving along that part, the ball will possess some magnitude of acceleration. And the distance covered at that part is,
\[d = ut + \dfrac{1}{2}a{t^2}\]
Here, u is the magnitude of initial speed and a is the magnitude of acceleration of the ball.
Now, for the lower horizontal part, we can observe that there is zero magnitude of acceleration of the ball. And the distance covered by the ball is the same as in the first case.
\[d = vt\]
Now by analysing the above conditions, the graph plotted in option D is correct and satisfies all the relevant conditions obtained as above.

Therefore, the graph D represents the graph for the distance travelled by the ball vs time graph and option (D) is correct.

Note: To resolve the given problem, one must try to clear the basics of linear motion. And also try to remember the fundamental formulas involved in analysing the linear motion. These formulas are used to calculate the typical problems of linear motion.