Question

A rigid body of mass m is moving in a circle of radius r with a constant speed \[v\]. The force on the body is \[\dfrac{m{{v}^{2}}}{r}\] and is directed towards the centre. What is the work done by this force in moving the body over half the circumference of the circle.

Answer 1

Hint:
As written in the question, the force is directed towards the center meaning the force is centripetal force. Hence, to find the work done by the mass m moving around a circle of radius r, we find the work done by the \[cos\] component of the product of force and displacement giving the formula for the work done as:
\[W=F.S\]
where F is the centripetal force, S is the distance covered.

Complete step by step solution:
Drawing a diagram for the rigid body mass to move around a circle of radius r as:

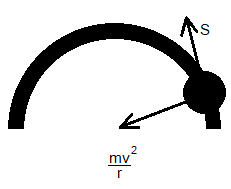
The force exerted by the mass is directed to the center of the pathway as done for in the case of centripetal force. Now if the particle is moving with a constant velocity then the rate of the movement of the particle with time given constant acceleration making the force positive and non-fluctuating. Hence, using the formula for work done is:
\[W=F.S\]
Now the components for the work done are both outside the circle and inside the circle. The work done component for inside the circle is:

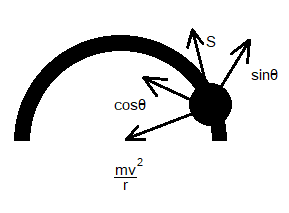
\[W=F.S\cos \theta \]
The work done component for outside the circle is
\[W=F.S\sin \theta \]
The component we need as the work done in case of centripetal force is directed outwards.
Hence, placing the angular value of the direction of distance and force as shown in the diagram and with \[\theta ={{90}^{\circ }}\], we get the work done as:
\[W=F.S\cos {{90}^{\circ }}\]
\[\Rightarrow W=0\]
Therefore, the work done in moving the particle around a circle is zero and is not dependent on the radius of the circle hence, for half a circle or full circle the work done is zero.

Note: The work done for any force that is perpendicular to the direction is motion is always zero, another example is when a person carries any object and moves in a straight line then the work done is zero irrespective of the person’s state after doing the work.