Question

A right-angled triangle, whose sides are 15cm and 20cm, is made to revolve about its hypotenuse. Find the volume and the surface area of the double cone so formed.
(a) $3878c{{m}^{3}},1315.8c{{m}^{2}}$
(b) $3777c{{m}^{3}},1312.8c{{m}^{2}}$
(c) $3788c{{m}^{3}},1310.8c{{m}^{2}}$
(d) $3768c{{m}^{3}},1318.8c{{m}^{2}}$

Answer 1

Hint: Calculate the hypotenuse of this triangle using the Pythagoras Theorem. Take the hypotenuse as the height of the double right circular cone. Calculate the perpendicular distance from the point joining the two sides of the triangle to the hypotenuse. This is the radius of the cone. Calculate the volume of the cone using the formula $\dfrac{1}{3}\pi {{r}^{2}}h$. Calculate the surface area of the cone by adding the curved surface area of upper and lower cones. To calculate the curved surface area of the cone, use the formula $\pi rl$.

Complete step-by-step answer:
We have to calculate the volume and surface area of the double cone that is formed by revolving the right-angled triangle along its hypotenuse whose sides are of length 15cm and 20cm.

Let’s consider that our right-angled triangle is $\Delta ABD$, right-angled at B, with $AB=15cm,BD=20cm$ and AD being the hypotenuse of the triangle, as shown in the figure.

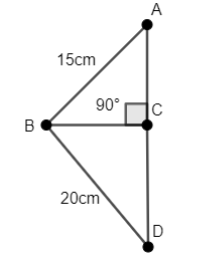
We will calculate the length of the hypotenuse AD using Pythagoras Theorem. We know that Pythagoras Theorem states that in a right-angled triangle, the sum of the square of two perpendicular sides is equal to the square of the third side.
Thus, we have ${{\left( AB \right)}^{2}}+{{\left( BD \right)}^{2}}={{\left( AD \right)}^{2}}$. Substituting $AB=15cm,BD=20cm$ in the previous formula, we have ${{\left( AD \right)}^{2}}={{15}^{2}}+{{20}^{2}}=225+400=625$.
Taking square root on both sides, we have $AD=\sqrt{625}=25cm$.
We will now calculate the radius of the cone, which is the length of side BC.
We observe that $\Delta ABC$ is right-angled at C. Thus, using Pythagoras Theorem, we have ${{\left( AC \right)}^{2}}+{{\left( BC \right)}^{2}}={{\left( AB \right)}^{2}}$. Substituting $AB=15cm$ in the previous equation, we have $A{{C}^{2}}+B{{C}^{2}}={{15}^{2}}=225.....\left( 1 \right)$.
Similarly, we observe that $\Delta BCD$ is right-angled at C. Thus, using Pythagoras Theorem, we have ${{\left( BC \right)}^{2}}+{{\left( CD \right)}^{2}}={{\left( BD \right)}^{2}}$. Substituting $BD=20cm$ in the previous equation, we have $B{{C}^{2}}+C{{D}^{2}}={{20}^{2}}=400.....\left( 2 \right)$.
We know that $AC+CD=AD=25cm$. Thus, we have $CD=25-AC.....\left( 3 \right)$.
Substituting equation (3) in equation (2), we have $B{{C}^{2}}+{{\left( 25-AC \right)}^{2}}=400$.
We know that ${{\left( x-y \right)}^{2}}={{x}^{2}}+{{y}^{2}}-2xy$. Thus, we can rewrite the above equation as $B{{C}^{2}}+A{{C}^{2}}+{{25}^{2}}-2\left( 25 \right)\left( AC \right)=400$.
So, we have $B{{C}^{2}}+A{{C}^{2}}-50AC=400-625=-225.....\left( 4 \right)$.
Subtracting equation (1) from equation (4), we have $B{{C}^{2}}+A{{C}^{2}}-50AC-\left( A{{C}^{2}}+B{{C}^{2}} \right)=-225-225$.
Thus, we have $-50AC=-450\Rightarrow AC=\dfrac{-450}{-50}=9cm.....\left( 5 \right)$.
Substituting equation (5) in equation (1), we have ${{9}^{2}}+B{{C}^{2}}=225\Rightarrow B{{C}^{2}}=225-81=144$.
Taking square root on both sides of the above equation, we have $BC=\sqrt{144}=12cm$.
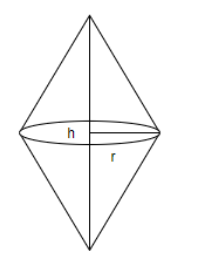
Thus, the radius and height of the cone are $BC=12cm$ and $AD=25cm$ respectively.
We will now calculate the volume of the cone. We know that the volume of the cone with radius ‘r’ and height ‘h’ is $\dfrac{1}{3}\pi {{r}^{2}}h$.
Substituting $r=12cm,h=25cm$ in the above formula, the volume of the double cone is $=\dfrac{1}{3}\pi {{\left( 12 \right)}^{2}}\left( 25 \right)=3768c{{m}^{3}}$.
We will now calculate the surface area of the cone. The surface area of the cone is the sum of the curved surface area of the upper and lower cone.
We know that the curved surface area of any cone with radius ‘r’ and slant height ‘l’ is $\pi rl$.
We will first calculate the curved surface area of the upper cone, formed by the triangle $\Delta ABC$. We know that the radius of this cone is $BC=12cm$ and $AB=15cm$. Substituting these values in the formula $\pi rl$, the curved surface area of the upper cone is $=\pi \left( 12 \right)\left( 15 \right)=565.2c{{m}^{2}}$.
We will now calculate the curved surface area of the lower cone, formed by the triangle $\Delta BCD$. We know that the radius of this cone is $BC=12cm$ and $BD=20cm$. Substituting these values in the formula $\pi rl$, the curved surface area of the lower cone is $=\pi \left( 12 \right)\left( 20 \right)=753.6c{{m}^{2}}$.
Thus, the total surface area of the cone is $=565.2c{{m}^{2}}+753.6c{{m}^{2}}=1318.8c{{m}^{2}}$.
Hence, the volume and total surface area of the cone is $3768c{{m}^{3}}$ and $1318.8c{{m}^{2}}$ respectively, which is option (d).

Note: We must keep in mind that this is a double cone. So, we have to add the surface area of both the upper and lower cone. One must also be careful about units while calculating the volume and total surface area of the cone. As the dimensions of the cone are in centimetres, the volume and total surface area will be in cubic centimetres and square centimetres.