Question

A right Triangle, whose sides are $3$ cm and $4$ cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone to form. (Choose the value of $\pi $ as found appropriate.)

Answer 1

Hint: For solving this question, first of all we will draw the diagram to get the cone. Then, we will use Pythagorean Theorem to calculate its hypotenuse. Then, we will use the formula of the area of the triangle to get the height of the cones. After that we will use the formula of volume of cone and formula of surface area of cone and will simplify to get the required answer.

Complete step-by-step solution:
Let’s consider that the right angle triangle as:

Now, we will get the new diagram after rotating it about its hypotenuse as:

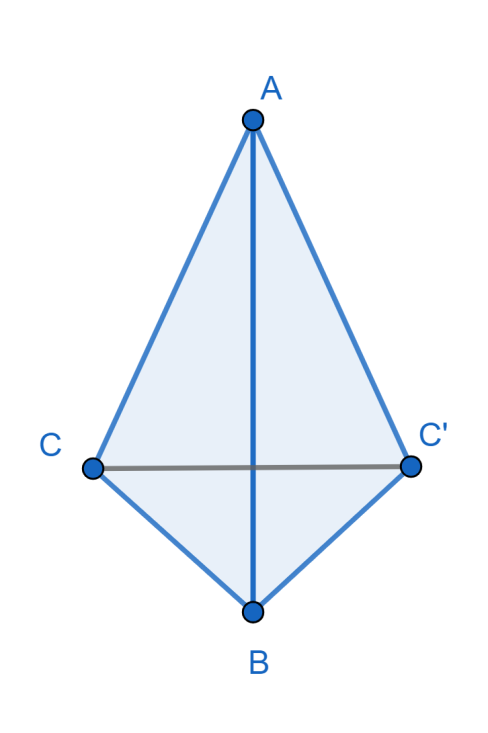
As, we can clearly see that there are two cones, one is $CBC'$ and another one is $CAC'$. Now, we will calculate the length of the height of the cones.
So, from the triangle, we have two sides. Then, we will use the formula of Pythagorean Theorem to calculate hypotenuse $AB$ as:
$\Rightarrow A{{B}^{2}}=B{{C}^{2}}+A{{C}^{2}}$
Now, substitute the corresponding value in the above formula to get the length of the hypotenuse.
$\Rightarrow A{{B}^{2}}={{3}^{2}}+{{4}^{2}}$
Here, we will square the both numbers as:
$\Rightarrow A{{B}^{2}}=9+16$
Now, we will add as:
$\Rightarrow A{{B}^{2}}=25$
After taking square root, we will have:
$AB=5$ cm.
Since, the line $AB$ and $CC'$ intersects each other perpendicularly at point $D$. So, we can use the formula of area of triangle to get the length of $CD$ as:

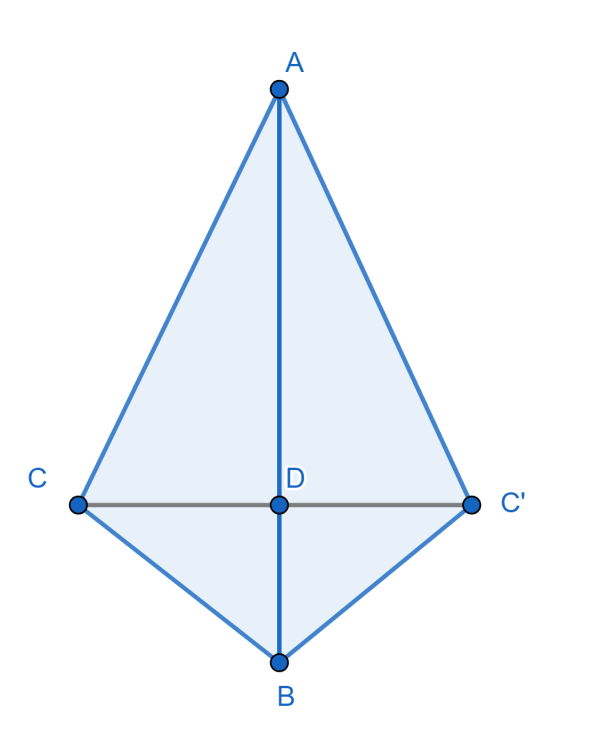
$\Rightarrow \dfrac{1}{2}\times AB\times CD=\dfrac{1}{2}\times BC\times AC$
Now, we will substitute the corresponding values and cancel out equal like term as:
$\Rightarrow 5\times CD=3\times 4$
Here, we will simplify it as:
$\begin{align}
  & \Rightarrow 5\times CD=12 \\
 & \Rightarrow CD=\dfrac{12}{5} \\
 & \Rightarrow CD=2.4 \\
\end{align}$
Now, we have a radius of cones that is $2.4$ cm.
So, we will use the formula to calculate the volume of double cone as:
$\Rightarrow \text{Volume of Double cone}=\text{Volume of first cone}\left( CAC' \right)\text{ }+\text{Volume of second cone}\left( CBC' \right)$
$\begin{align}
  & \Rightarrow \text{Volume of Double cone}=\text{ }\dfrac{1}{3}\times \pi \times C{{D}^{2}}\times AD\text{ }+\text{ }\dfrac{1}{3}\times \pi \times C{{D}^{2}}\times BD \\
 & \Rightarrow \text{Volume of Double cone}=\text{ }\dfrac{1}{3}\times \pi \times C{{D}^{2}}\left[ AD\text{ }+\text{ }BD \right] \\
\end{align}$
We can see that $AD+BD=AB$. So, the above equation will be as:
$\Rightarrow \text{Volume of Double cone}=\text{ }\dfrac{1}{3}\times \pi \times C{{D}^{2}}\times AB$
Now, substitute the corresponding values as:
$\Rightarrow \text{Volume of Double cone}=\text{ }\dfrac{1}{3}\times 3.14\times {{\left( 2.4 \right)}^{2}}\times 5$
After doing the required calculation, we will have:
$\begin{align}
  & \Rightarrow \text{Volume of Double cone}=\text{ }\dfrac{1}{3}\times 15.7\times 5.76 \\
 & \Rightarrow \text{Volume of Double cone}=\text{ }15.7\times 1.82 \\
 & \Rightarrow \text{Volume of Double cone}\approx \text{ }28.574\text{ }c{{m}^{3}} \\
\end{align}$
Now, we will calculate the surface area of the double cone as:
$\begin{align}
  & \Rightarrow \text{Surface area of Double cone} =\text{Surface area of first cone }\left( CAC' \right)\text{ }+\text{surface area of second cone}\left( CBC' \right) \\
 & \Rightarrow \text{Surface area of Double cone}=\pi \times CD\times AC\text{ }+\text{ }\pi \times CD\times BC \\
\end{align}$Here, we will substitute the corresponding values as:
$\begin{align}
  & \Rightarrow \text{Surface area of Double cone}=\pi \times CD\times \left( AC\text{ }+\text{ }BC \right) \\
 & \Rightarrow \text{Surface area of Double cone}=3.14\times 2.4\times \left( 4\text{ }+\text{ }3 \right) \\
\end{align}$
Now, we will simplify it as:
$\begin{align}
  & \Rightarrow \text{Surface area of Double cone}=7.536\times 7 \\
 & \Rightarrow \text{Surface area of Double cone }\approx 52.752\text{ }c{{m}^{2}} \\
\end{align}$
Hence, the volume of double cone and surface area of double cone is $28.574$ cm cube and $52.752$ cm square respectively.

Note: A cone is a $3D$ diagram that has a radius $\left( r \right)$ , height $\left( h \right)$ and the slant height $l$ from a horizontal base to a point on the top of it. The formula for the volume of the cone is $\dfrac{1}{3}{{\pi }^{2}}h$ and the formula of the surface area of the cone is $\pi rl$.