Question

A right triangle has a hypotenuse of length \[p\] cm and one side of length \[q\] cm. If \[p - q = 1\] , find the length of the third side of the triangle if \[p = 5\] and \[q = 4\]

Answer 1

Hint: To solve this question, to calculate the third side of a right-angled triangle we use the Pythagoras theorem.

Complete step-by-step answer:
               

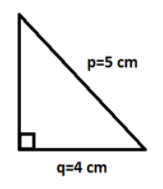
In the question, it is given that the hypotenuse is of length \[p\] cm and one side is of length \[q\] cm.
So, Hypotenuse \[ = p\] cm and Base \[ = q\] cm as shown in the figure.
So, now we will use Pythagoras theorem.
Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.“ The sides of this triangle have been named as Perpendicular, Base and Hypotenuse.
So, \[Hypotenus{e^2} = Bas{e^2} + Perpendicula{r^2}\]
\[{p^2} = {q^2} + Perpendicula{r^2}\]
\[Perpendicula{r^2} = {p^2} - {q^2}\]
Now, we will put \[p = 5\] and \[q = 4\] in the above formed equation, we get
\[Perpendicula{r^2} = {5^2} - {4^2}\]
Or, \[Perpendicula{r^2} = 25 - 16\]
Or, \[Perpendicula{r^2} = 9\]
Therefore, \[Perpendicular = 3\]
Thus, the length of the third side of the triangle is equal to \[3\] cm.

Note: Keep in mind the Pythagoras theorem. The Pythagorean equation relates the sides of a right triangle in a simple way, so that if the lengths of any two sides are known the length of the third side can be found. Another corollary of the theorem is that in any right triangle, the hypotenuse is greater than any one of the other sides, but less than their sum.