Question

A right cone is $5.4\,cm$ high and radius is $2\,cm$ . It is melted and recast into another cone of radius $1.5\,cm$ . Find the height of the new cone.

Answer 1

Hint: The given question is related to the volume of cones. The volume of the cone before and after melting and recasting will be the same. To find the height of the new cone, first, find the volume of the first cone. Then, assume the height of the new cone as $h$ . Then, find the volume of the new cone in terms of $h$ and equate it to the initial volume to find the value of $h$ .
Complete step-by-step answer:

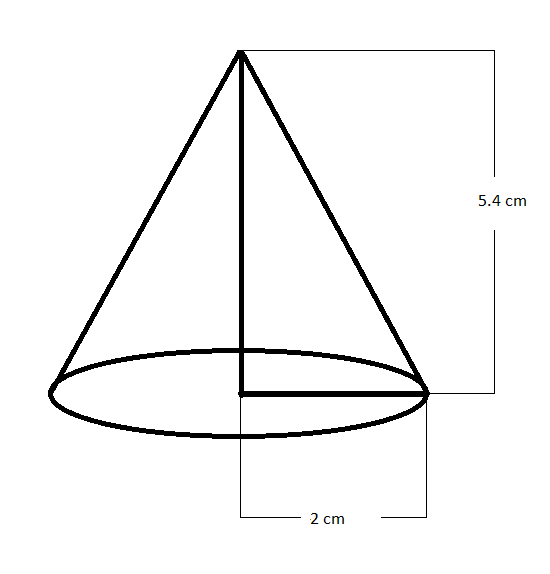
We are given the initial height of the cone as $5.4\,cm$ and the initial radius of the cone as $2\,cm$ . We know, the volume of a cone with height $h$ and radius $r$ is given as $V=\dfrac{1}{3}\pi {{r}^{2}}h$ . So, the volume of the initial cone will be equal to ${{V}_{i}}=\dfrac{1}{3}\pi {{(2)}^{2}}\left( 5.4 \right)\,c{{m}^{3}}$, which is equal to $7.2\pi \,c{{m}^{3}}$ .
Now, we do not know the height of the new cone. So, let’s assume it to be equal to $h\,cm$. The radius of the new cone is given as $1.5\,cm$ . So, the volume of the new cone is given as ${{V}_{f}}=\dfrac{1}{3}\pi {{\left( 1.5 \right)}^{2}}h\,c{{m}^{3}}$ , which is equal to $0.75h\pi \,c{{m}^{3}}$ .
Now, we are given that the initial cone is melted and recast into the new cone. So, their volumes must be equal, i.e. ${{V}_{i}}={{V}_{f}}$ .
So, $7.2\pi =0.75h\pi $
$\Rightarrow 7.2=0.75h$
$\Rightarrow h=\dfrac{7.2}{0.75}=9.6$
Hence, the height of the new cone is $9.6\,cm$.

Note: While solving problems related to areas and volumes, always make sure that the units of the dimensions are the same. If the units are not the same then, use the unit conversion relations to make the units same. Mathematical operations cannot be performed between two entities with different units. Students generally do not care for the units and make calculations without ensuring that the units are the same and end up getting a wrong answer.