Question

A right circular cylindrical tower height \[h\] and radius \[r\] stands on the ground. Let \[P\] be a point in the horizontal plane ground and ABC are the semicircular edge of the top of the tower such that B is the point in it nearest to \[P\] . The angles of elevation of the points A and B are 45° and 60° respectively. Show that \[\dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {1 + \sqrt 3 } \right)}}{2}\].

Answer 1

Hint: We will draw a figure to represent the situation given in the question. We will find the value of \[h\] and \[r\] using standard trigonometric ratios. We will compute \[\dfrac{h}{r}\] and simplify the equation to get the desired form.

Formulas used:
In a right angled triangle \[\tan \theta = \dfrac{P}{B}\] where \[P\] is the perpendicular of the triangle and \[B\]is the base of the triangle.
\[\tan {60^ \circ } = \sqrt 3 \]
\[\tan {45^ \circ } = 1\]
\[\left( {a - b} \right)\left( {a + b} \right) = {a^2} - {b^2}\]

Complete step-by-step answer:
We will draw a figure for the question:

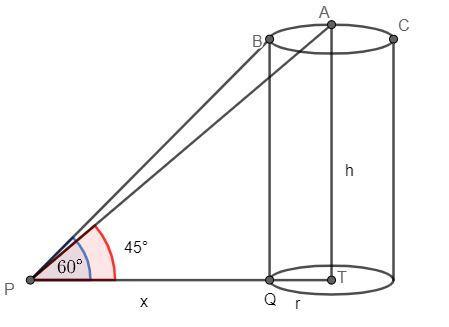
Both \[AT\] and \[BQ\] have length \[h\].
We will assume that the length of \[PQ\]is \[x\].
In \[\Delta BPQ\], \[BQ\] is the perpendicular and \[PQ\] is the base. We will use the first and second formula to find \[\dfrac{h}{x}\] :
\[\begin{array}{c}\tan {60^ \circ } = \dfrac{{BQ}}{{PQ}}\\\tan {60^ \circ } = \dfrac{h}{x}\\\left( 1 \right){\rm{ }}\sqrt 3 = \dfrac{h}{x}\end{array}\]
We can see from the figure that \[PT = x + r\]
In \[\Delta PAT\], \[AT\]is the perpendicular and \[PT\]is the base. We will use the first and third formula to find \[x\]:
\[\tan {45^ \circ } = \dfrac{{AT}}{{PT}}\\\Rightarrow \tan {45^ \circ } = \dfrac{h}{{x + r}}\\ \Rightarrow 1 = \dfrac{h}{{x + r}}\\x + r = h\\\Rightarrow \left( 2 \right){\rm{ }}x = h - r\]
We will substitute \[h - r\] for \[x\] in the first equation:
\[\sqrt 3 = \dfrac{h}{{h - r}}\]
We will cross multiply \[h - r\] with \[\sqrt 3 \] :
\[\Rightarrow \sqrt 3 \left( {h - r} \right) = h\\\Rightarrow \sqrt 3 h - \sqrt 3 r = h\\ \Rightarrow \sqrt 3 h - h = \sqrt 3 r\\ \Rightarrow h\left( {\sqrt 3 - 1} \right) = \sqrt 3 r\\ \Rightarrow \dfrac{h}{r} = \dfrac{{\sqrt 3 }}{{\sqrt 3 - 1}}\]
We will multiply the numerator and the denominator in the right-hand side with\[\left( {\sqrt 3 + 1} \right)\] to convert the denominator into rational form:
\[\Rightarrow \dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}\]
We will substitute \[\sqrt 3 \] for \[a\] and 1 for \[b\] in the 4th formula:
\[ \Rightarrow \begin{array}{l}\dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{{{{\left( {\sqrt 3 } \right)}^2} - 1}}\\ \Rightarrow \dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{2}\end{array}\]
\[\therefore \] We have shown that \[\dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{2}\].
Note: We can also find the solution by cross multiplying \[x\] with \[\sqrt 3 \] in the 1st equation:
\[\begin{array}{c}\sqrt 3 x = h\\x = \dfrac{h}{{\sqrt 3 }}\end{array}\]
We will substitute \[\dfrac{h}{{\sqrt 3 }}\] for \[x\] in the 2nd equation:
\[\Rightarrow \dfrac{h}{{\sqrt 3 }} = h - r\\ \Rightarrow \dfrac{h}{{\sqrt 3 }} - h = r\\h\left( {\dfrac{1}{{\sqrt 3 }} - 1} \right) = r\]
We will take the L.C.M.:
\[\Rightarrow h\left( {\dfrac{{1 - \sqrt 3 }}{{\sqrt 3 }}} \right) = r\\\Rightarrow \dfrac{h}{r} = \dfrac{{\sqrt 3 }}{{1 - \sqrt 3 }}\]
We will multiply the numerator and the denominator in the right-hand side with\[\Rightarrow \left( {\sqrt 3 + 1} \right)\] to convert the denominator into rational form:
\[\Rightarrow \dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}\]
We will substitute \[\sqrt 3 \] for \[a\] and 1 for \[b\] in the 4th formula:
\[ \Rightarrow \dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{{{{\left( {\sqrt 3 } \right)}^2} - 1}}\\\Rightarrow \dfrac{h}{r} = \dfrac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{2}\]
We have proven the desired result.