Question

: A right circular cylinder just encloses a sphere of radius r (see below figure). Find the
(i) Surface area of the sphere.
(ii) Curved surface area of the cylinder.
(iii) Ratio of surface areas obtained in (i) and (ii).

Answer 1

Hint: A right circular cylinder is a cylinder whose base is a circle and whose elements are perpendicular to its base. Here, the height of the cylinder and diameter of the sphere are the same.
Formulas used: Surface area of a sphere is $4\pi {r^2}$ where ‘r’ is the radius of the sphere and \['\pi '\] is equal to 22/7 or 3.14.
Curved surface area of the cylinder is $2\pi rh$ where ‘r’ is the radius of the base of the cylinder and ‘h’ is the height of the cylinder.

Complete step-by-step answer:

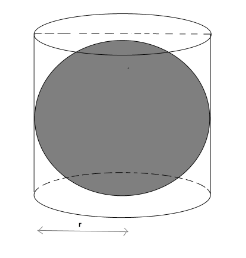
Given that the right circular cylinder encloses a sphere of radius r.
From the figure, we get that the diameter of the sphere and height of the cylinder are the same and also the diameter of the sphere and the diameter of the base of the cylinder are the same.
Given that the radius of the sphere is ‘r’ which means the diameter of the sphere is ‘2r’.
Therefore, the height of the cylinder is ‘2r’ and radius of the base of the cylinder is ‘r’. $ \to statement1$
(i) Surface area of the sphere
Surface area of the sphere is $4\pi {r^2}$
As we know that the radius of the sphere given is ‘r’, the surface area of the sphere is the same which is $4\pi {r^2}$ .
(ii)Curved surface area of the cylinder
Curved surface area of the cylinder is $2\pi rh$
h=2r and r=r from the statement 1.
Finally curved surface area of the cylinder
 $
   = 2 \times \pi \times r \times 2r \\
   = 2 \times 2 \times \pi \times r \times r \\
   = 4\pi {r^2} \\
$
(iii) Ratio of surface areas obtained in (i) and (ii)
Ratio of surface area of the sphere and curved surface area of the cylinder =
Surface area of the sphere/Curved surface area of the cylinder
Surface area of the sphere obtained is $4\pi {r^2}$ .
Curved surface area of the cylinder obtained is $4\pi {r^2}$ .
 Therefore, the ratio is
$
   = \dfrac{{4\pi {r^2}}}{{4\pi {r^2}}} \\
   = \dfrac{1}{1} \\
   = 1:1 \\
$
Therefore, the ratio of the surface area of the sphere and curved surface area of the cylinder is 1:1.

Note: A Circle is a two-dimensional figure whereas a Sphere is a three-dimensional object. So do not confuse a sphere with a circle.A right circular cylinder is a cylinder that has a closed circular surface having two parallel bases on both the ends and are perpendicular to its base. It is also known as a right cylinder.