Question

A right circular cone is divided by a plane parallel to its base in two equal volumes. In what ratio will the plane divide the axis of the cone.

Answer 1

Hint: To find the ratio the plane will divide the axis of the cone, first draw a cone and cut it parallel to the base and then you will get a smaller cone and a frustum, then equate the volumes of the cone and the frustum. When equating, use similar triangle properties to further evaluate the equation and also use the formula of difference between cube of two numbers to further simplify the equation and get the required ratio.

Complete step by step solution:
Let us consider a cone $ {\text{VAB}} $ having its height $ h $ and base radius $ r $ , now dividing the cone with a plane parallel to its base which makes a smaller cone $ {\text{VA'B'}} $ having height $ {h_1} $ and base radius $ {r_1} $ as follows

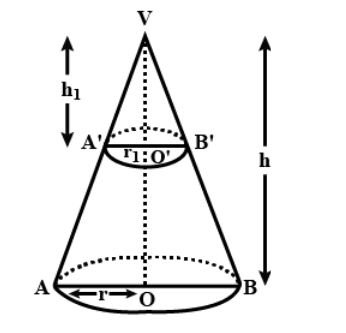
Now, in order to find the ratio in which the plane cuts the cone in equal volume, we will equate the volume of the smaller cone and the frustum
Volume of cone $ {\text{VA'B'}} = $ Volume of the frustum $ {\text{ABB'A'}} $
 $
   \Rightarrow \dfrac{1}{3}\pi r_1^2{h_1} = \dfrac{1}{3}\pi \left( {{r^2} + r_1^2 + r{r_1}} \right)\left( {h - {h_1}} \right) \\
   \Rightarrow r_1^2{h_1} = \left( {{r^2} + r_1^2 + r{r_1}} \right)\left( {h - {h_1}} \right) \;
  $
Dividing $ r_1^2\;{\text{and}}\;{h_1} $ both sides we will get
 $ \Rightarrow 1 = \left( {\dfrac{{{r^2}}}{{r_1^2}} + 1 + \dfrac{r}{{{r_1}}}} \right)\left( {\dfrac{h}{{{h_1}}} - 1} \right) $
Now we can see in the figure that $ \Delta {\text{VA'B'}}\;{\text{and}}\;\Delta {\text{VAB}} $ are similar, so we can write
 $ \dfrac{r}{{{r_1}}} = \dfrac{h}{{{h_1}}} $
Using this we can write,
\[ \Rightarrow 1 = \left( {\dfrac{{{h^2}}}{{h_1^2}} + 1 + \dfrac{h}{{{h_1}}}} \right)\left( {\dfrac{h}{{{h_1}}} - 1} \right)\]
Simplifying this,
\[
   \Rightarrow 1 = {\left( {\dfrac{h}{{{h_1}}}} \right)^3} - {1^3} \\
   \Rightarrow {\left( {\dfrac{h}{{{h_1}}}} \right)^3} = 1 + 1 \\
   \Rightarrow \dfrac{h}{{{h_1}}} = \sqrt[3]{2} \;
 \]
Hence the ratio \[\dfrac{{{h_1}}}{{h - {h_1}}} = \dfrac{1}{{\dfrac{{h - {h_1}}}{{{h_1}}}}} = \dfrac{1}{{\dfrac{h}{{{h_1}}} - 1}} = \dfrac{1}{{\sqrt[3]{2} - 1}}\]
\[1:\sqrt[3]{2} - 1\] is the required ratio.
So, the correct answer is “\[1:\sqrt[3]{2} - 1\]”.

Note: When considering the variables, select wisely how it will help you in further calculation and if it will give the required outcomes or not. Also drawing a diagram for this type of problems is a good habit, it gives you more imagination and thinking to solve the problem quickly.