Question

A right circular cone has height $ 9\text{ cms} $ and radius of the base $ 5\text{ cms} $ . It is inverted and water is poured into it. If at any instant the water level rises at the rate of $ \left( \dfrac{\pi }{A} \right)\text{cms/}{\sec } $ where A is the area of water surface at that instant. Show that the vessel will be full in 75 seconds.

Answer 1

Hint: We first assume the radius of the water surface and the height of the water at a particular moment and express that through image form. We have to find the area of the water surface and then replace the value with $ \dfrac{dh}{dt}=\left( \dfrac{\pi }{A} \right) $ . Then we use integration to find the relation between height and radius and place the value of $ h=9 $ to find the answer.

Complete step by step answer:
We first try to express the given information about the cone in the image form. The inverted right circular cone has height $ 9\text{ cms} $ and radius of the base $ 5\text{ cms} $ .

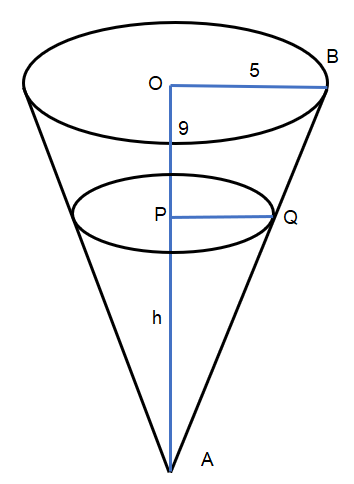
So, the height being OA and the radius being OB, we can say $ OA=9, OB=5 $ .
Now we assume the radius of the water surface and the height of the water at a particular moment. Let them be r and h respectively. So, $ PQ=r,PA=h $ .
At any instant the water level rises at the rate of $ \left( \dfrac{\pi }{A} \right)\text{cms/}{\sec } $ where A is the area of water surface at that instant. This means $ \dfrac{dh}{dt}=\left( \dfrac{\pi }{A} \right) $ .
For the assumed water level, the area of the surface area of the water will be $ A=\pi {{r}^{2}}\text{ c}{{\text{m}}^{2}} $ .
The triangles $ \Delta OAB $ and $ \Delta PAQ $ are similar as the angles are equal.
Therefore, the ratios of the sides are equal which gives $ \dfrac{r}{h}=\dfrac{5}{9} $ .
To put the value of r in the equation of $ A=\pi {{r}^{2}} $ , we get $ r=\dfrac{5h}{9} $ .
So, $ A=\pi {{r}^{2}}=\pi {{\left( \dfrac{5h}{9} \right)}^{2}}=\dfrac{25\pi {{h}^{2}}}{81} $ .
We put the value of A in $ \dfrac{dh}{dt}=\left( \dfrac{\pi }{A} \right) $ and get $ \dfrac{dh}{dt}=\left( \dfrac{\pi }{A} \right)=\dfrac{81\pi }{25\pi {{h}^{2}}}=\dfrac{81}{25{{h}^{2}}} $ .
Now we try to form the differential of h and t for integration and get $ \Rightarrow {{h}^{2}}dh=\dfrac{81}{25}dt $ .
We find the integration of the equation.
 $ \begin{align}
  & \Rightarrow \int{{{h}^{2}}dh}=\dfrac{81}{25}\int{dt} \\
 & \Rightarrow \dfrac{{{h}^{3}}}{3}=\dfrac{81}{25}t+c \\
\end{align} $
Here c is the integral constant.
For initial part we had for $ t=0 $ value of $ h=0 $ . So, $ 0=0+c\Rightarrow c=0 $ .
Therefore, the relation is $ 25{{h}^{3}}=243t $ .
We need to find the time for the vessel to be full which means $ h=9 $ .
We get $ \Rightarrow t=\dfrac{25{{h}^{3}}}{243}=\dfrac{25\times {{\left( 9 \right)}^{3}}}{243}=75 $ .
Thus, proved that the vessel will be full in 75 seconds.

Note:
The rate of the area changing for a certain height given. That’s why we used the value of r with respect to the height. The solution can also be solved using the radius part also. The differential form represents the instantaneous change of height for a particular moment which on integration gives the relation.