Question

A right angled triangle has a hypotenuse, base and a perpendicular side. Let angle A be the angle between the base and the hypotenuse. Draw and find sin A

Answer 1

Hint: The problem can be solved by constructing a right angled triangle and using the sine of the angle formula, between the base and the hypotenuse to calculate the required ratio of the sides.

Complete step by step solution: Given below shows the right angle triangle ABC.

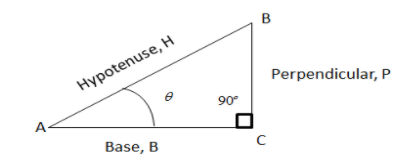
ABC is aright angled triangle, right angled at C. The side AC is the base which is a horizontal side. AB is t called the hypotenuse, which is the inclined and longest side of the triangle while the side BC is called the altitude or perpendicular side of the triangle. The perpendicular is the shortest side of a right angled triangle.
The important thing related to any right angled triangle is that Pythagoras theorem is applicable. It is a theorem that relates the three sides of a right angled triangle. According to the theorem, the square of the hypotenuse is equal to the square of the base plus the square of the perpendicular.
In right angled triangle ABC, applying Pythagoras theorem
$A{B^2} = B{C^2} + A{C^2}$
${H^2} = {B^2} + {P^2}$
$H = \sqrt {{B^2} + {P^2}} $
In the right angled triangle, sine of the angle is the ratio of the side which is opposite to the angle to the hypotenuse.
$
  A{B^2} = B{C^2} + A{C^2} \\
  AB = \sqrt {B{C^2} + A{C^2}} \cdots (1) \\
 $
The sine of angle A is given by,
$
  \sin A = \dfrac{P}{H} \\
  \sin A = \dfrac{{AC}}{{AB}} \cdots (2) \\
 $
Substituting the value of AB in equation (2)
$\sin A = \dfrac{{AC}}{{\sqrt {B{C^2} + A{C^2}} }}$

Note: The important steps are
 (i) The use of Pythagoras theorem for the evaluation of hypotenuse in terms of base and perpendicular.
(ii) The sine of the angle is the ratio of the opposite side of the angle to the hypotenuse.