Question

A right angle triangle has hypotenuse of length p cm and one side of length q cm. If $p - q = 1$, find the length of the third side of the triangle.

Answer 1

Hint: Given triangle is a right angle triangle. So use Pythagoras theorem, to find the unknown length of the side of the triangle. Also use appropriate algebraic identities to get the required length.

Complete step-by-step answer:

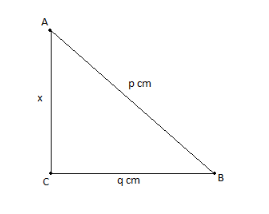
We are given a right angle triangle has hypotenuse of length p cm and one side has a length q cm.
In a right angled triangle, by Pythagoras theorem the square of hypotenuse is equal to the sum of squares of the remaining two adjacent sides.
Here the length of the hypotenuse is p cm and one side length is q cm; let the length of the remaining side be ‘x’ cm.

Let the given triangle be ABC
Therefore, $A{B^2} = A{C^2} + B{C^2}$
$
  {p^2} = {q^2} + {x^2} \\
  {x^2} = {p^2} - {q^2} \\
  {x^2} = \left( {p + q} \right)\left( {p - q} \right) \\
  \left( {\because {a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)} \right) \\
 $
Substitute the value $p - q = 1$ in the above equation.
$
  {x^2} = \left( {p + q} \right)\left( 1 \right) \\
  p - q = 1 \to p = 1 + q \\
 $
Substitute the value of p in the place of p.
$
  {x^2} = \left( {1 + q + q} \right) \\
  {x^2} = 1 + 2q \\
  x = \sqrt {1 + 2q} cm \\
 $
Therefore, the length of the third side x is $\sqrt {1 + 2q} $ cm.
In a right angles triangle, if the hypotenuse is p cm and one side is q cm then the length of the third side is $\sqrt {1 + 2q} $cm.

Note: The right angled triangle has one angle 90 degrees and the remaining two acute angles. Sum of the interior angles of a triangle is 180 degrees. So to compensate the 180 degrees there will be only one right angle possible in a triangle. A right angle triangle is responsible for all the trigonometric functions.