Question

A right angle triangle ABC having right angle at C, CA = a, CB = b moves such that the angular points A and B slide along x – axis and y – axis respectively. The locus of C is:
(a) ax + by + 1 = 0
(b) $ax\pm by=0$
(c) $a{{x}^{2}}\pm 2by+{{y}^{2}}=0$
(d) None of these.

Answer 1

Hint:We will take the point C as some variable (x,y) and then the points A and B are also variable points on the x and y axis. Then we find the slope of AC and BC, and it is given that they are perpendicular from that we will get an equation and then we will use the distance formula showing CA = a and CB = b. And hence from this we will find the locus of C.

Complete step-by-step answer:
Let the points be,
A = (h,0)
B = (0,k)
C = (x,y)

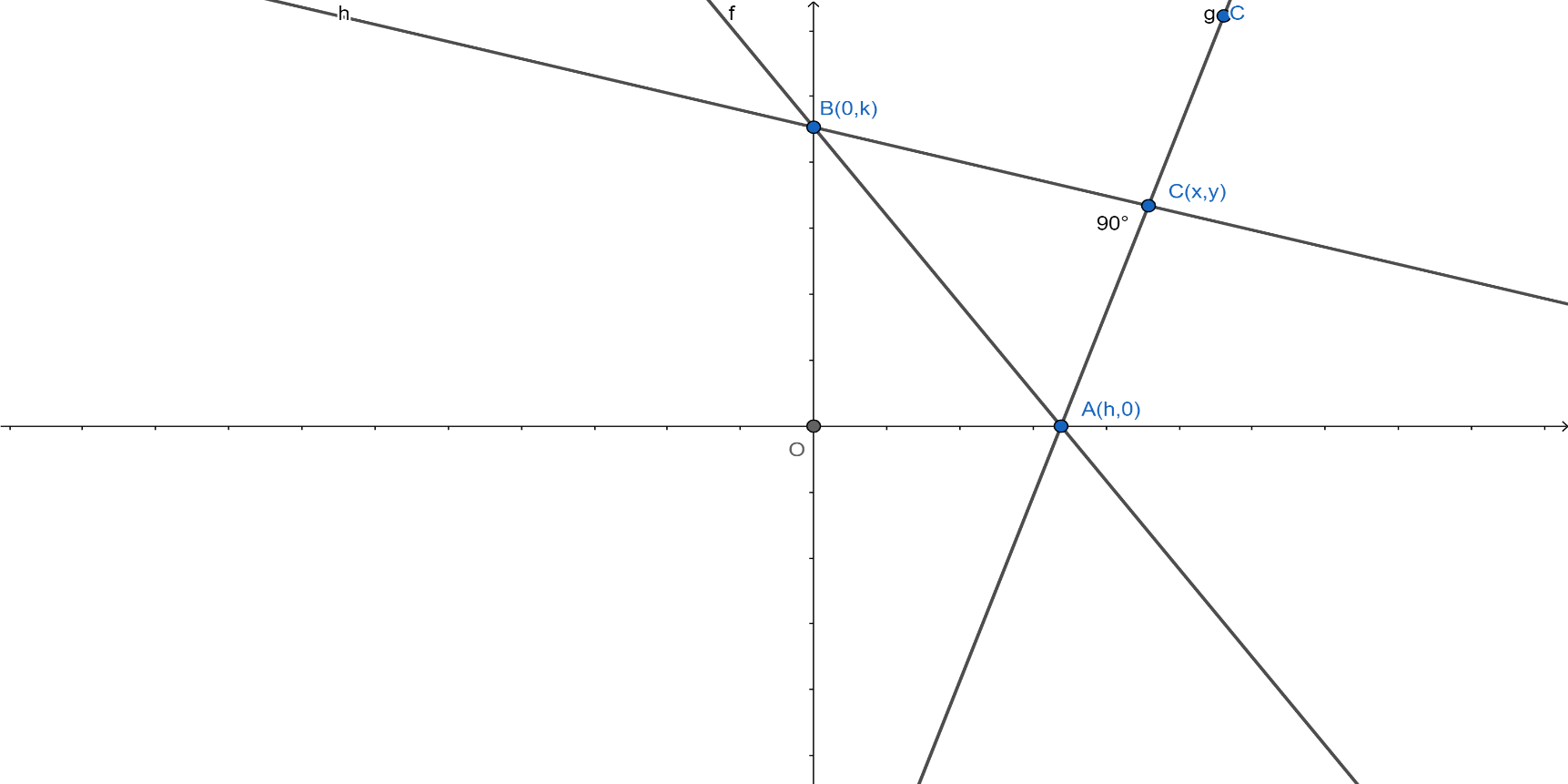
Now we will find the slope of AC which is ${{m}_{1}}$ ,
${{m}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\dfrac{y-0}{x-h}$
Now we will find the slope of BC which is ${{m}_{2}}$ ,
${{m}_{2}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\dfrac{y-k}{x-0}$
Now we know that AC and BC are perpendicular,
Therefore, ${{m}_{1}}{{m}_{2}}=-1$
$\begin{align}
  & \left( \dfrac{y}{x-h} \right)\left( \dfrac{y-k}{x} \right)=-1 \\
 & y\left( y-k \right)+x\left( x-h \right)=0................(1) \\
\end{align}$
Now it is given that CA = a and CB = b,
Therefore, we will use the distance formula $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ in CA and CB,
Therefore, we get
$\begin{align}
  & CA=a=\sqrt{{{\left( x-h \right)}^{2}}+{{\left( y-0 \right)}^{2}}} \\
 & {{a}^{2}}={{\left( x-h \right)}^{2}}+{{y}^{2}} \\
 & x-h=\sqrt{{{a}^{2}}-{{y}^{2}}} \\
\end{align}$
Similarly we get,
$\begin{align}
  & CB=b=\sqrt{{{\left( x-0 \right)}^{2}}+{{\left( y-k \right)}^{2}}} \\
 & {{b}^{2}}={{\left( y-k \right)}^{2}}+{{x}^{2}} \\
 & y-k=\sqrt{{{b}^{2}}-{{x}^{2}}} \\
\end{align}$
Now we will substitute the value of x – h and y – k in (1),
Therefore we get,
$y\left( \sqrt{{{b}^{2}}-{{x}^{2}}} \right)+x\left( \sqrt{{{a}^{2}}-{{y}^{2}}} \right)=0$
$\begin{align}
  & y\left( \sqrt{{{b}^{2}}-{{x}^{2}}} \right)=-x\left( \sqrt{{{a}^{2}}-{{y}^{2}}} \right) \\
 & {{y}^{2}}\left( {{b}^{2}}-{{x}^{2}} \right)={{x}^{2}}\left( {{a}^{2}}-{{y}^{2}} \right) \\
 & {{y}^{2}}{{b}^{2}}-{{x}^{2}}{{y}^{2}}={{a}^{2}}{{x}^{2}}-{{x}^{2}}{{y}^{2}} \\
 & {{y}^{2}}{{b}^{2}}-{{x}^{2}}{{a}^{2}}=0 \\
\end{align}$
Now using the formula $\left( {{a}^{2}}-{{b}^{2}} \right)=\left( a-b \right)\left( a+b \right)$ we get,
$\left( by-ax \right)\left( by+ax \right)=0$
Therefore, from this we get two solutions,
$ax+by=0$ and $ax-by=0$
Hence, taking the two solution together we get,
$ax\pm by=0$
Hence option (b) is correct.

Note: All the formulas that we have used like the distance formula $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ and ${{m}_{1}}{{m}_{2}}=-1$ when the slopes are perpendicular, all these are very important formula and must be kept in mind while solving the question.