Question

A rhombus sheet, whose perimeter is $32$ m and whose one diagonal is $10$ m long,
is painted on both sides at the rate of $5$ per ${{\rm{m}}^2}$.Find the cost of painting.
A. ${\rm{Rs}}{\rm{.630}}$
B. ${\rm{Rs 625}}$
C. ${\rm{Rs 312}}{\rm{.24}}$
D. ${\rm{Rs 62}}{\rm{.44}}$

Answer 1

Hint: In this problem it is given that a rhombus sheet, whose perimeter is $32$ m and whose
diagonal is $10$ m long, and is painted on both sides of a at the rate of $5$ per ${{\rm{m}}^2}$.
We have to find the cost of painting. Firstly, we have considered a rhombus ABCD where AC
and BD are diagonals of rhombus and then find the area of rhombus.

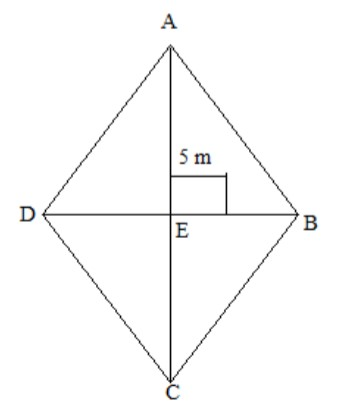
It is given that perimeter of rhombus is $32$ m and whose one diagonal $10$ m long is painted
on both sides at the rate of ${\rm{rs}}{\rm{. }}5$ per meter square. We have to find the cost of
painting.
Let us consider a rhombus ABCD.
Now, use the formula of perimeter of rhombus to find the side of rhombus.
Perimeter of rhombus ABCD$ = 4 \times {\rm{AB}}$
$\begin{array}{l} \Rightarrow 32{\rm{m}} = 4 \times {\rm{AB}}\\ \Rightarrow {\rm{AB =
8m}}\end{array}$
Since, AC is diagonal given length is $10$ m.
So, ${\rm{AE}} = \dfrac{{{\rm{AC}}}}{2} = \dfrac{{10}}{2} = 5$ m
In $\Delta {\rm{ABC}}$,
Since, AEB is at a right angle.
By Pythagoras Theorem, we get
$ \Rightarrow {\rm{A}}{{\rm{B}}^2} = {\rm{A}}{{\rm{E}}^2} + {\rm{E}}{{\rm{B}}^2}$
Substitute $8$ for AB and $5$ for AE in the above expression.
$\begin{array}{l} \Rightarrow 64 = 25 + {\rm{E}}{{\rm{B}}^2}\\ \Rightarrow
{\rm{E}}{{\rm{B}}^2} = 39\\ \Rightarrow {\rm{EB}} = \sqrt {39} \end{array}$
Also, ${\rm{BD}} = 2{\rm{EB}}$
Therefore, ${\rm{BD}} = {\rm{2}}\sqrt {39} $ m
Now, Area of rhombus$ = \dfrac{1}{2} \times {\rm{product of diagonals}}$
\[\begin{array}{l}{\rm{ = }}\dfrac{1}{2} \times {\rm{AC}} \times
{\rm{BD}}\\{\rm{ = }}\dfrac{1}{2} \times 10 \times 2\sqrt {39} \\ = 10\sqrt {39}
{{\rm{m}}^2}\end{array}\]
To determine the area of the painted side as it painted from both the sides.
Area of the painted side$ = 2 \times 10\sqrt {39} = 20\sqrt {39} $
Since it is given rate of painting is ${\rm{Rs}}{\rm{.5 }}{{\rm{m}}^2}$
Thus, cost of painting $ = {\rm{Rs }}20\sqrt {39} \times 5$

$\begin{array}{l} = {\rm{Rs 100}}\sqrt {39} \\ = {\rm{Rs }}100 \times
6.245\\ = {\rm{Rs 624}}{\rm{.5}}\\ \approx {\rm{ Rs 625}}\end{array}$
Hence, the correct answer is B.
Note: Here we have considered a rhombus ABCD where AC and BD are diagonals for which we have found the area of rhombus. Also we have-AEB is a right angle triangle. By applying
Pythagoras theorem, we find another diagonal. Since it is given rate of painting is
${\rm{Rs}}{\rm{.5 }}{{\rm{m}}^2}$, then we get the final answer.