Question

A rhombus is a quadrilateral that has four congruent sides. How would you prove that the diagonals of a rhombus intersect at a point that is the midpoint of each diagonal?

Answer 1

Hint: We are given a rhombus that has four congruent sides. We have to prove that diagonals of a rhombus intersect at the midpoint of each diagonal. First, draw the figure to show the rhombus and its diagonals. Then, show that diagonals of rhombus are perpendicular to each other. Then, apply the theorem of the perpendicular bisector.

Complete step by step solution:
Draw the figure of rhombus ABCD and join the diagonals.

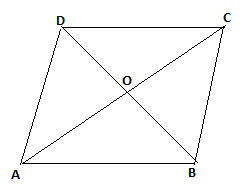
Given that the sides of the rhombus are equal.

$ \Rightarrow AB = BC = CD = AD$

Now, in triangles $\Delta AOB$ and $\Delta BOC$

$ \Rightarrow OA = OC$ (Because diagonals of parallelogram will bisect each other in two equal parts)

$ \Rightarrow OB = OB$ (Common side of the triangles)

$ \Rightarrow AB = CB$(Because $AB = BC = CD = AD$)

Therefore, by SSS congruence

$\Delta AOB \cong \Delta BOC$

Using the congruent part of the congruent triangle,

$ \Rightarrow \angle AOB = \angle BOC$ ……(1)

Apply the linear pair property of angle, we get:

$ \Rightarrow \angle AOB + \angle BOC = 180^\circ $

Using equation (1), substitute the $\angle AOB$ for $\angle BOC$, we get:

$ \Rightarrow \angle AOB + \angle AOB = 180^\circ $

$ \Rightarrow 2\angle AOB = 180^\circ $

Divide both sides by 2, we get:

$ \Rightarrow \angle AOB = 90^\circ $

From equation (1), we get:

$ \Rightarrow \angle BOC = 90^\circ $

Also, apply the property of vertical opposite angles to $\angle AOB$

$ \Rightarrow \angle AOB = \angle COD$

Therefore, $\angle COD = 90^\circ $

Similarly, apply the property of vertical opposite angles to $\angle BOC$

$ \Rightarrow \angle BOC = \angle DOA$

Therefore, $\angle DOA = 90^\circ $

Therefore, $\angle AOB = \angle BOC = \angle COD = \angle DOA = 90^\circ $

Thus, we can say that diagonals are perpendicular to each other.

$ \Rightarrow AC \bot BD$

Now, we will apply the perpendicular bisector definition, which states that perpendicular bisector intersects another line perpendicularly and divides the line segment into two equal parts.

Here, AC divided the line BD into two equal parts and also BD divides the line segment AC into two equal parts. Thus, we can say that the diagonals intersect each other at midpoint.


Note: The students must remember the following properties of congruence of the triangles for such types of questions:
SSS congruence means side- side – side
SAS congruence property is side- angle- side
AAS congruence property is Angle-Angle-side
ASA congruence property is Angle-side-Angle