Question

A resonant AC circuit contains a capacitor of capacitance $10^{-6}F$ and an inductor of $10^{-4}H$. The frequency of the oscillations will be:
\[\begin{align}
  & A{{.10}^{5}}Hz \\
 & B.10Hz \\
 & C.\dfrac{{{10}^{5}}Hz}{2\pi } \\
 & D.\dfrac{10Hz}{2\pi } \\
\end{align}\]

Answer 1

Hint: We know that the source of an AC circuit is sinusoidal. Then there is a phase difference between the voltage and current. If the phase difference between the current and voltage is zero, then both are said to be in phase, and if the phase difference is not equal to zero, then both are said to be out of phase.

Formula used:
 $\omega=\dfrac{1}{\sqrt{LC}}$

Complete step-by-step answer:
When the natural frequency of the system matches the applied frequency, then there is an increase in amplitude, then the system is said to experience resonance.
Similarly, when an AC current is passed through a LCR circuit, then the circuit experiences resonance. This is observed when the reactance due to the capacitance and the inductance are equal and opposite, thus cancel each other.

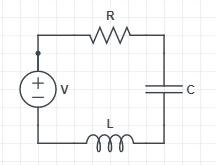
Then, we can say $X_{L}=X_{C}$, where $X_{L}, X_{C}$ is the reactance due to the inductance and the capacitance respectively.
$2\pi fL=\dfrac{1}{2\pi fC}$
$\Rightarrow f^{2}=\dfrac{1}{4\pi^{2} LC}$
$\Rightarrow f=\sqrt{\dfrac{1}{{4\pi^{2} LC}}}$
$\Rightarrow f=\dfrac{1}{2\pi\sqrt{LC}}$
$\Rightarrow \omega=\dfrac{1}{\sqrt{LC}}$
Then the maximum angular frequency given as $\omega=\dfrac{1}{\sqrt{LC}}$, where $L$ is the inductor and $C$ is the capacitance.
Here it is given that, $L=10^{-4}H$ and $C=10^{-6}F$
Then, the resonance angular frequency $\omega$ will become,$\omega=\dfrac{1}{\sqrt{10^{-4}\times 10^{-6}}}=\dfrac{1}{\sqrt{10^{-10}}}=10^{5}$
We also know that $\omega=2\pi f$, where $f$ is the frequency.
Then we get resonance frequency is given as $f=\dfrac{10^{5}}{2\pi}$
Hence the answer is \[C.\dfrac{{{10}^{5}}Hz}{2\pi }\]

So, the correct answer is “Option C”.

Note: Resonance is observed when RLC is connected in series. Not when RLC is in parallel connection, or in RL, RC or LC circuit. In an RLC connection the impedance is called purely real, as only R is active in the circuit and there is no impedance in the circuit. For frequency less than the resonant frequency, the impedance is capacitive in nature and for frequency greater than the resonant frequency, the impedance is inductive in nature.