Question

A resonance tube is old and has a jagged end. It is still used in the laboratory to determine velocity of sound in air. A tuning fork of frequency 512 Hz produces first resonance when the tube is filled with water to a mark 11 cm below a reference mark, near the open end of the tube. The experiment is repeated with another fork of frequency 256 Hz which produces first resonance when water reaches a mark 27 cm below the reference mark. The velocity of sound in air, obtained in the experiment, is close to:
A. $328m/s$
B. $322m/s$
C. $341m/s$
D. $335m/s$

Answer 1

Hint:
1. Velocity of sound is constant in a given medium.
2. First resonance frequency occurs for air column length, $l = \dfrac{\lambda }{4}$ in ideal scenarios.
3. End correction must be added to the path length of first resonance frequency.

Formula Used:
1. Distance between two consecutive nodes $ = \dfrac{\lambda }{2}$ …… (a)
2. Distance between Antinode and next successive node $ = \dfrac{\lambda }{4}$ ……. (b)
3.First resonance frequency with air column of length ${l_{air}} + e = \dfrac{\lambda }{4}$ ……. (c)
where $e$ is end correction
4. Constant speed of sound wave with $f$ be frequency of tuning fork and $\lambda $ be wavelength of sound wave $v = \lambda f$ $ \Rightarrow \lambda = \dfrac{v}{f}$ …… (d)
Figure 1 shows rough sketch for first resonance air column:

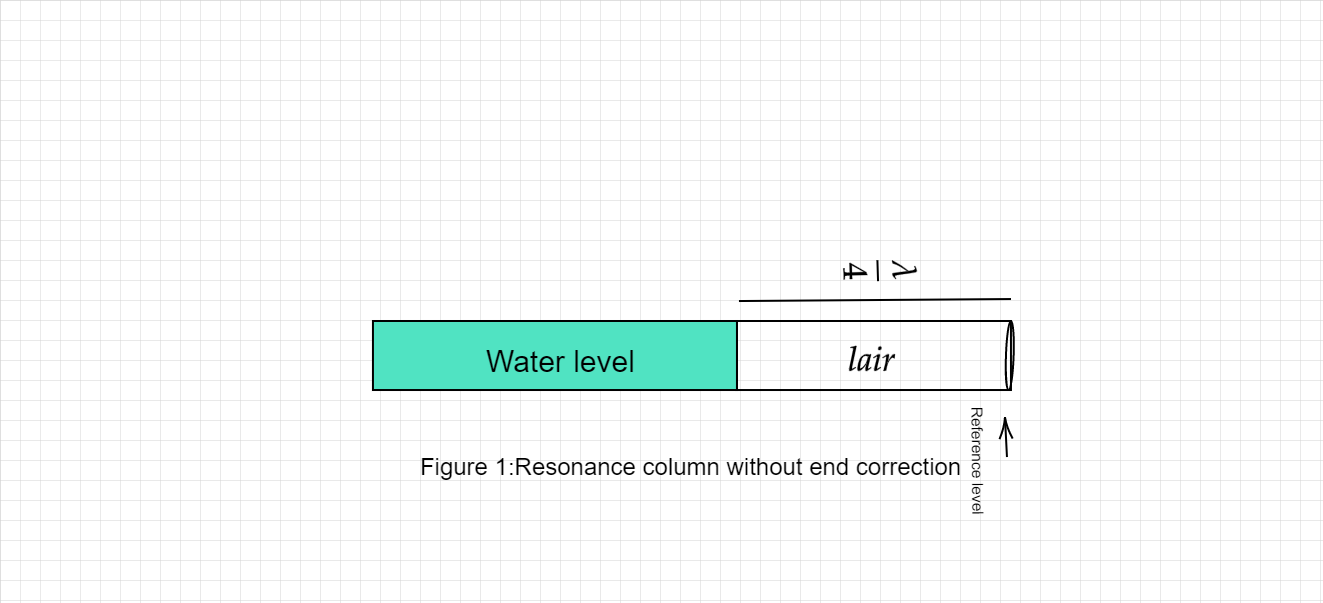
Complete step by step answer:

Given,
Two tuning forks of frequencies ${f_1}$ and ${f_2}$ be 512 Hz and 256 Hz respectively.
Corresponding to each frequency’s paths, the lengths of the first resonance air column are 11cm and 27 cm respectively.

Let, end correction be $e$

Step 1 of 4:

Using equation (c) and (b) for frequency ${f_1}$=512 Hz we get
$\dfrac{{{\lambda _1}}}{4} = {l_{1,air}} + e$ …… (1)
Given ${l_{air}} = 11cm$,
Putting substitutions from equation (1) and (d) we get,
$\dfrac{v}{{4 \times {f_1}}} = 11cm + e$ …… (2)

Step 2 of 4:

Similarly, using equation (c) and (b) for frequency ${f_2}$ =256 Hz we get
$\dfrac{{{\lambda _2}}}{4} = {l_{2,}}_{air} + e$ …… (3)
Putting substitutions from equation (1) and (d) we get,
$\dfrac{v}{{4 \times {f_2}}} = 27cm + e$ …… (4)

Step 3 of 4:

Subtracting equation (2) from equation (4) we get,
$\dfrac{v}{{4 \times {f_2}}} - \dfrac{v}{{4 \times {f_1}}} = 27cm + e - 11cm + e$
$ \Rightarrow \dfrac{v}{4}\left( {\dfrac{1}{{{f_2}}} - \dfrac{1}{{{f_1}}}} \right) = 16 \times {10^{ - 2}}m$ …… (5)

Step 4 of 4:

Putting values of ${f_1}$ and ${f_2}$ in equation (5) we get,
$v = 328m/s$

Correct Answer: A.$328m/s$

Additional Information: At the opening of a vessel there always lies an antinode. There lies a node at the interface between air and fluid since the fluid boundary acts as a closed vessel because at that point no displacement is possible.

Note: End correction should always be considered while solving sound wave problems in a vessel or tube.