Question

A rectangular water tank is 90 cm wide and 40 cm deep. If it can contain 576 litres of water, what is its length?

Answer 1

Hint: Use the formula, volume of cuboid to find the length of the tank. we have been given that it can contain 576 litres, which is basically the volume. Now that we have two dimensions, we can easily find the length by substituting the values in the formula. Use the formula of volume of cuboid V = l x b x h.

Complete step by step solution:
Write down the given measurements of the water tank, the width and the depth and the volume of the rectangular water tank. Consider width as ‘w’, depth as ‘d’ and volume of the tank as ‘V’. The figure below is the cuboid with the measurements, w = 90 cm, d = 40 cm and V = 576 litres.

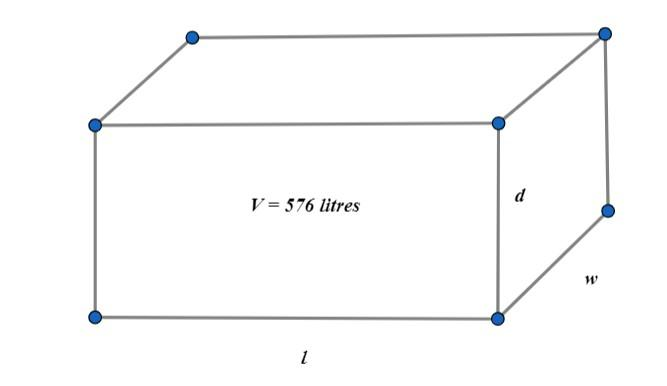
Convert the value of the volume from litres into $c{{m}^{3}}$.
We know that, $1\,litre=1000\,c{{m}^{3}}$
Multiply 576 by 1000 to get the volume in $c{{m}^{3}}$and we get,
$\begin{align}
  & V=576\,litres \\
 & =576\times {{10}^{3}}\,c{{m}^{3}}
\end{align}$
Now, use the formula volume of a cuboid, V = l x b x h
Here the breadth is considered as width and height as depth of the water tank.
Therefore, the formula changes to V = l x w x d
Substitute the given measurements of the water tank and solve the equation to find the length of the tank.
$\begin{align}
  & 576\times {{10}^{3}}=l\times 90\times 40 \\
 & \dfrac{576\times {{10}^{3}}}{90\times 40}=l \\
\end{align}$
Solve the following to find the value of length of the water tank.
l = 160 cm.
Hence, the value of the length of the water tank is 160 cm.

Note: In this problem, the conversion of the volume from litres into cubic centimeters is important because if you do not convert, you will get the wrong answer. While solving the equation make sure you consider the ${{10}^{3}}$which you used to convert the volume from litres into cubic centimeters.