Question

A rectangular vessel is of 2m long, 0.5m breadth, and 1m deep. If water flows in at the rate of 90 cubic cm per sec, then the rate of increase of water level when 25cm deep is
A. 0.09 cm/sec
B. 0.1 cm/sec
C. 0.01 cm/sec
D. 0.5 cm/sec

Answer 1

Hint: The given rectangular tank is a cuboid, so find the volume of the cuboid where volume is generally referred to as the capacity it has, or it can hold. A rectangle has a length and width to it, and its height is multiplied to it, then it becomes a cuboid.

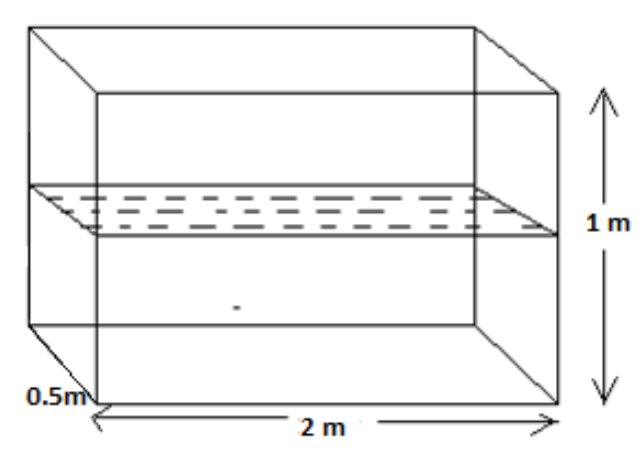
In this question, the dimensions of the vessel are given; hence find the total capacity or volume of the vessel and find the difference of volume of the water level when the water is 25cm deep and then find the rate of increase of water for that increased height of the water level.

Complete step by step answer:
 To start with, the first thing is to convert all the give dimensions in a common measuring unit. So, the meter is converted to centimeters by multiplying the number with 100. Hence,
Length \[l = 2m = 200cm\]
Breadth \[b = 0.5m = 50cm\]
Height \[h = 1m = 100cm\]
The volume of the cuboid is the product of the length, breadth, and height.
Substitute $l = 200{\text{ cm;}}b = 50{\text{ cm;}}h = 100{\text{ cm}}$ in the formula ${V_c} = l \times b \times h$ to determine the volume of the rectangular vessel (cuboid) as:

\[
  {V_c} = l \times b \times h \\
   = 200 \times 50 \times 100 \\
   = 1000000{\text{ }}c{m^3} - - - - (i) \\
 \]
Now the volume of the water when the height of the liquid in the vessel is 25cm deep (\[h' = 25cm\]) is given as:
\[
  {V_W} = l \times b \times h' \\
   = 200 \times 50 \times 25 \\
   = 250000{\text{ }}c{m^3} - - - - (ii) \\
 \]
According to the question, the rate of flow of water is $r = 90{\text{ }}c{m^3}{\sec ^{ - 1}}$.
Hence, the time is taken to fill the vessel up to a height of 25 cm is given as:
\[
  t = \dfrac{{{V_c}}}{r} \\
   = \dfrac{{250000{\text{ }}c{m^3}}}{{90{\text{ }}c{m^3}{{\sec }^{ - 1}}}} \\
   = 2777.7\sec \\
 \]
Now to determine the rate of change in the water level is given as the ratio of the required water level to the time taken by the pipe to fill the vessel up to that level at the rate of $r = 90{\text{ }}c{m^3}{\sec ^{ - 1}}$. Hence,
\[
  r' = \dfrac{{25{\text{ }}cm}}{{2777.7{\text{ sec}}}} \\
   = 0.009{\text{ }}cm{\text{ }}{\sec ^{ - 1}} \\
 \]
Hence, the rate of increase in water level when 25cm deep is 0.09 cm/sec, Option A is correct.

Note: Students should not get confused with the term rate of increase in the water level. It means that when the level of the water in the tank is 25 meter deep then, what is the rate of change in the level of the water. Moreover, 1 meter is the total height of the vessel (we don’t have to do anything here with this height), and 25 cm is the height of the water level at which the rate is to be determined.