Question

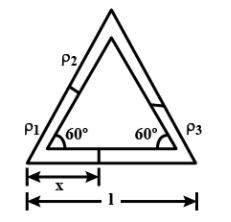
A rectangular tube of uniform cross-section has three liquids of densities ${\rho}_{1}$, ${\rho}_{2}$ and ${\rho}_{3}$. Each liquid column has length l equal to the length of sides of the equilateral triangle. Find the length x of the liquid density ${\rho}_{1}$ in the horizontal limb of the tube, if the triangular tube is kept in the vertical plane.

Answer 1

Hint: Consider the base of the equilateral triangle. Find the pressure at one end. And then, the pressure at the other end of the base. As it has uniform cross-section and the length of each side is the same, pressure at both the ends of the base is the same. Thus, equate the expression for pressure at both the ends. Then, substitute the value of heights in the obtained expression. Thus, obtain the value of length x.

Complete answer:
Let the base of the triangle i.e. the horizontal surface be AB.
Pressure is given by,
$P=\rho gh$ …(1)
Where, $\rho$ is the density of liquid
              h is the height
Using equation. (1), pressure at point A will be,
${ P }_{ A }={ \rho }_{ 1 }g{ h }_{ 1 }+{ \rho }_{ 2 }g{ h }_{ 2 }$
Similarly, pressure at point B will be,
${ P }_{ B }={ \rho }_{ 2 }g{ h }_{ 2 }^{ ' }+{ \rho }_{ 3 }g{ h }_{ 3 }$
But, the pressure at point is equal to that at point B.
$\Rightarrow { P }_{ A }={ P }_{ B }$ …(2)
Substituting the values in above expression we get,
$ {\rho }_{ 1 }g{ h }_{ 1 }+{ \rho }_{ 2 }g{ h }_{ 2 }={ \rho }_{ 2 }g{ h }_{ 2 }^{ ' }+{ \rho }_{ 3 }g{ h }_{ 3 }$
${ \rho }_{ 1 }{ h }_{ 1 }+{ \rho }_{ 2 }{ h }_{ 2 }={ \rho }_{ 2 }{ h }_{ 2 }^{ ' }+{ \rho }_{ 3 }{ h }_{ 3 }$ …(3)
Substituting values in the equation. (3) we get,
${ \rho }_{ 1 }(l-x)+{ \rho }_{ 2 }x={ \rho }_{ 2 }(l-x)+{ \rho }_{ 3 }x$
$\Rightarrow { \rho }_{ 1 }l-{ \rho }_{ 1 }x+{ \rho }_{ 2 }x={ \rho }_{ 2 }l-{ \rho }_{ 2 }x+{ \rho }_{ 3 }x$
$\Rightarrow x{ \rho }_{ 2 }-x{ \rho }_{ 1 }+x{ \rho }_{ 2 }-x{ \rho }_{ 3 }=l{ \rho }_{ 2 }-l{ \rho }_{ 1 }$
$\Rightarrow x{ (\rho }_{ 2 }-{ \rho }_{ 1 }+{ \rho }_{ 2 }-{ \rho }_{ 3 })=l({ \rho }_{ 2 }-{ \rho }_{ 1 })$
$\Rightarrow x=\dfrac { l(\rho _{ 2 }-{ \rho }_{ 1 }) }{ { (\rho }_{ 2 }-{ \rho }_{ 1 }+{ \rho }_{ 2 }-{ \rho }_{ 3 }) }$
$\Rightarrow x=\dfrac { l(\rho _{ 2 }-{ \rho }_{ 1 }) }{ { (2\rho }_{ 2 }-{ \rho }_{ 1 }-{ \rho }_{ 3 }) }$
Therefore, length x is $\dfrac { l(\rho _{ 2 }-{ \rho }_{ 1 }) }{ { (2\rho }_{ 2 }-{ \rho }_{ 1 }-{ \rho }_{ 3 }) }$

Note: From equation. (1), it can be inferred that pressure is directly proportional to density of the liquid. As the density of liquid or height increases, pressure on the liquid also increases and when density decreases, pressure decreases. When the pressure increases, molecules of substance come closer and thus density increases. Density is inversely proportional to temperature. As the temperature increases, liquid expands. Thus, the density decreases.