Question

A rectangular tank $30cm\times 20cm\times 12cm$ contains water to a depth of 6cm. A metal cube of side 10cm is placed in the tank with its one face resting on the bottom of the tank. Find the volume of water, in litre, that must be poured into the tank so that the metal cube is just submerged in the water.
(a) 1.4 litre
(b) 1.3 litre
(c) 1.2 litre
(d) 1 litre

Answer 1

Hint: First, we will find volume of water in the tank using the formula $length\times breadth\times height\text{ }of\text{ }water$ . Then, we will find the volume of the cube by using the formula ${{\left( length \right)}^{3}}$ . Then, we will find the total volume in the tank by summation of volume of cube and volume of water in the tank. So, we will have total volume in the tank. From this we will find a new height ‘h’ of water by which total volume we got. After getting h, we will subtract it from the height of the cube and that will be our final height. Then again finding the volume of water using that height will be our final answer.

Complete step by step solution:
Here, we are given dimensions of a rectangular tank i.e. $30cm\times 20cm\times 12cm$ where length is 30cm, breadth is 20cm and height of tank is 12cm. Height of the tank is 6cm. Figure is as shown below.

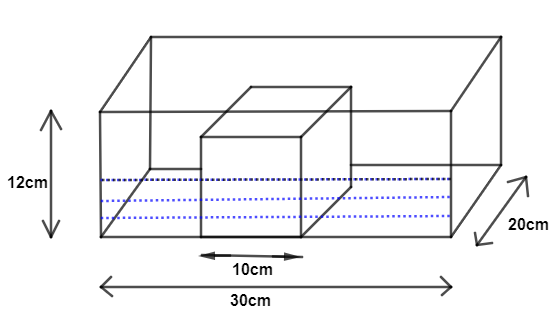
Blue dotted lines are taken to be water whose height is 6cm.
So, we will find the volume of water in the tank given as $length\times breadth\times height\text{ }of\text{ }water$ . We will get as
Volume of water in tank $=30\times 20\times 6$
$=3600c{{m}^{3}}$ ………………………………..(1)
 Now, we will find the volume of the cube whose side length is 10cm using the formula ${{\left( length \right)}^{3}}$ . So, we will get as
Volume of cube $={{\left( length \right)}^{3}}={{\left( 10 \right)}^{3}}=1000c{{m}^{3}}$ ……………………………(2)
Now, the total volume in a rectangular tank is equal to summation of volume of water and volume to cube. We can write this as
$\text{total volume in tank=volume of water+volume of cube}$
On putting values, we get as
$\text{total volume in tank=3600+1000=4600c}{{\text{m}}^{3}}$ ……………………………….(3)
Now, we know that the height of the cube is 10cm and the total volume in the tank is $\text{4600c}{{\text{m}}^{3}}$ . So, we have to find how much height ‘h’ is increased in water in the tank, so the volume is $\text{4600c}{{\text{m}}^{3}}$ . We can write it as
$30\times 20\times h=4600$
On solving this, we will get as
$600\times h=4600$
$h=\dfrac{4600}{600}=7.667cm$ ……………………….(4)
Now, we will subtract this height from the height of the cube, so we will get $10-7.667=2.333cm$ .
So, the volume of water to be poured is $length\times breadth\times height\text{ }of\text{ }water$ i.e.
Volume of water to be poured in tank $=30\times 20\times 2.333$
$=1399.8c{{m}^{3}}$
$\approx 1.4c{{m}^{3}}$
Hence, option (a) is the correct answer.


Note: Another approach to solve this problem is by finding how much volume of water level has increased by placing the metal cube. So, we will get $10\times 10\times 6=600c{{m}^{3}}$ . Then by finding surface area of tank and surface area of cube we will get as $30\times 20=600c{{m}^{2}}$ and $10\times 10=100c{{m}^{2}}$ respectively. So, on subtracting we will get the remaining surface area to be $500c{{m}^{2}}$ . So, we will find an increase in height by multiplying surface area with height h and equating it with volume we found. We will get as $500\times h=600$ . So, we will get $h=1.2cm$ . Thus, total water level height is $6+1.2=7.2cm$ . Then as we have done in solution remains the same. We will get the answer.