Question

A rectangular strip \[25\text{ cm}\times \text{7 cm}\] is rotated about the longer side. Find the volume of the solid, thus generated.

Answer 1

Hint: For this question, we will first start by drawing the rectangular strip of the measurements \[25\text{ cm}\times \text{7 cm}\] and then rotate it along the longer side of the given strip and then generate the figure which will be a cylinder. After that we will find the volume of the cylinder as asked in the question by applying: $\pi {{r}^{2}}h$.

Complete step by step answer:

We are given that there is a rectangular strip \[25\text{ cm}\times \text{7 cm}\] which looks like as follows:

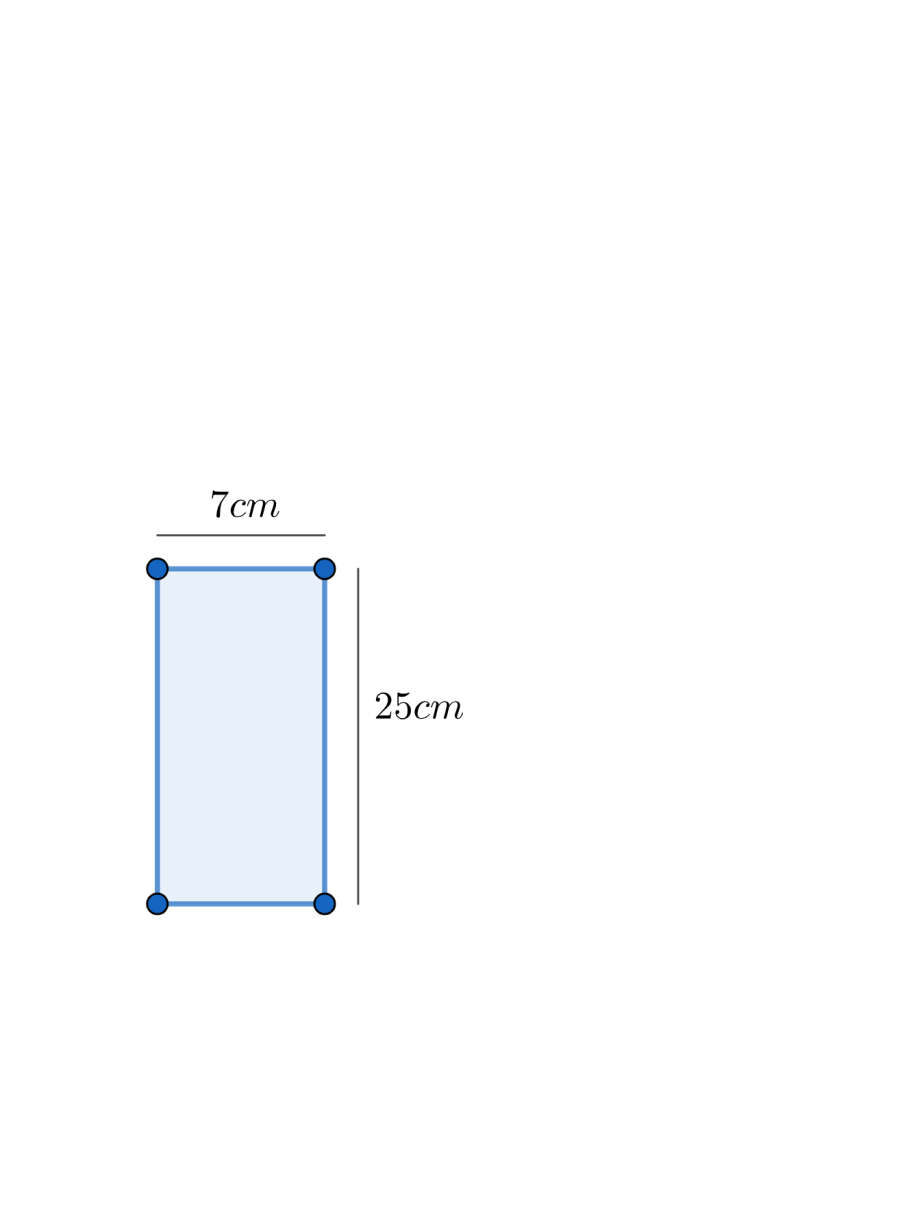
Now we will rotate it along the longer side that is $25\text{ cm}$ which will give us a cylinder of height $25\text{ cm}$ and radius $7\text{ cm}$ , which will look like following:

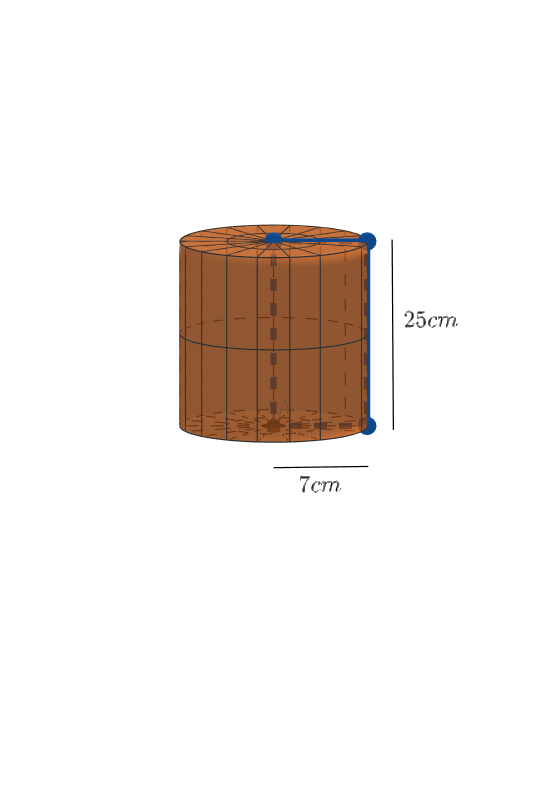
Now, the volume of a cylinder is the density of the cylinder which signifies the amount of material it can carry or how much amount of any material can be immersed in it. It is given that we have to find the volume of the obtained figure, now we know that the formula of volume of cylinder is: $\pi {{r}^{2}}h$ , where $r$ is the radius of cylinder and $h$ is the height of cylinder. So, we now have the cylinder of height $25\text{ cm}$ and radius $7\text{ cm}$:
Therefore, $V=\pi {{r}^{2}}h\Rightarrow V=\left( \dfrac{22}{7}\times {{\left( 25 \right)}^{2}}\times 7 \right)=13750\text{ c}{{\text{m}}^{3}}$
Hence, the answer is $13750\text{ c}{{\text{m}}^{3}}$.

Note:
In these types of questions, we need to have a proper visualization so that we don’t get confused about the figure thus generated. Always mention the units after getting the answer that is cubic units for the volume and square units for the area. You can also take $\pi \text{ as 3}\text{.141}$.