Question

A rectangular sheet of paper is $12\dfrac{1}{2}cm$ long and $10\dfrac{2}{3}cm$ wide. Find its perimeter.

Answer 1

Hint: first we will convert the given dimensions i.e. length and breadth into normal fraction form so, we will get as $l=\dfrac{25}{2}cm$ and $b=\dfrac{32}{3}cm$ . Then, we will use the formula to find perimeter as $2\left( length\times breadth \right)$ . So, we will get the answer.

Complete step-by-step answer:
Here, we are given the length and breadth of a rectangular sheet of paper denoted as $l=12\dfrac{1}{2}cm$ and $b=10\dfrac{2}{3}cm$ respectively. We get figure as below:

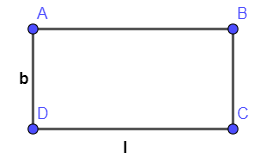
So, we will convert mixed fraction form, into fraction form.
So, we will convert mixed fraction form, into fraction form. Basically, mixed fractions are in the form of $quotient\dfrac{remainder}{divisor}$ . So, to convert it into fraction form we have to multiply $\left( divisor\times quotient \right)+remainder$ . By this we will get a fraction in the form of $\dfrac{dividend}{divisor}$ .
So, we will get length as $\dfrac{\left( 12\times 2 \right)+1}{2}$ i.e. $l=\dfrac{25}{2}cm$ and breadth as $\dfrac{\left( 10\times 3 \right)+2}{3}$ i.e. $b=\dfrac{32}{3}cm$ .
Now, we know that perimeter means summation of all 4 sides. So here, perimeter $=AB+BC+CD+AD$
Here, $AD=BC=b$ and $AB=CD=l$ . So, we can with formula as
Perimeter $=2\left( AB+AD \right)$
$=2\left( l+b \right)$
Now, we will substitute the values so, we will get
$=2\left( \dfrac{25}{2}+\dfrac{32}{3} \right)$
We will take LCM inside the brackets. We will get as
$=2\left( \dfrac{25\times 3+32\times 2}{6} \right)$
On further solving, we will get as
$=2\left( \dfrac{75+64}{6} \right)$
$=\left( \dfrac{139}{3} \right)=46.33cm$
Thus, the perimeter of the rectangular sheet of paper is 46.33 cm.

Note: Another method to solve this is by not converting mixed fraction to normal fraction. We can write $l=12\dfrac{1}{2}cm$ as 12.5 cm because we know $\dfrac{1}{2}=0.5$ and $b=10\dfrac{2}{3}cm$ as 10.66 because we know $\dfrac{2}{3}=0.66$ . So, length is 12.5 and breadth is 10.66. So, putting this value into the formula we will get the same answer.