Question

A rectangular sheet of paper ABCD is divided by 2 lines, each of which it cuts its length and breadth into 2 equal parts respectively. Find the area of any one small
(a) $\dfrac{1}{4}\left( \text{Area of ABCD} \right)$
(b) $\dfrac{1}{8}\left( \text{Area of ABCD} \right)$
(c) $\dfrac{1}{2}\left( \text{Area of ABCD} \right)$
(d) None of these

Answer 1

Hint: We will first find the area of rectangle ABCD which we know that is $length\times breadth$ . Then, we will draw a line such that the rectangle is divided into two parts whose length will be half of its original length. Then, again we will draw a line such that its breadth is divided into two equal parts whose breadth is half of its original breadth. Then we will find the area of the rectangle with this new length and breadth obtained after cutting the original rectangle. On comparing this area with the original area, we will get the answer.

Complete step-by-step answer:
Here, we will first draw a rectangle with length l and breadth b.

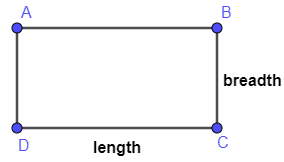
So, we know that area of rectangle ABCD is given as $A=l\times b$ . ……………………….(1)
Now, if we cut length in two equal parts, we will have two rectangles ADFE and EFCB given as below:

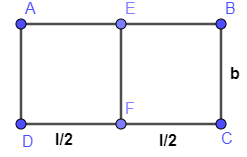
Now, as both the rectangles are equal, we will find the area of any one rectangle i.e. let us take ADFE. Here length is half i.e. $\dfrac{l}{2}$ and breadth b is the same. So, area will be
$A1=\dfrac{l}{2}\times b=\dfrac{lb}{2}$ ………………………….(2)
Now, we will draw a line in which breadth is cut into two equal parts. Figure is as given below:

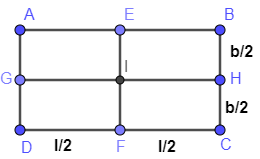
Now, we are asked to find the area of any one rectangle after length and breadth are cut into two equal parts. So, here we will find an area of AGIE whose length and breadth are $\dfrac{l}{2},\dfrac{b}{2}$ respectively. So, we get
$A2=\dfrac{l}{2}\times \dfrac{b}{2}=\dfrac{lb}{4}$ ………………………………(3)
We will compare area of rectangle ABCD and rectangle AGIE which we can say that
$\dfrac{lb}{4}=lb$
$\dfrac{1}{4}\left( \text{Area of ABCD} \right)=lb$
Thus, option (a) is the correct answer.

Note: Another approach to solve this type of problem is by assuming length and breadth as any number as any integer value. And then solving this as a solution, we will get the same answer. There are chances of calculation mistakes happening in this type of problem. So, do not make this mistake.