Question

A rectangular sheet of paper \[66cm \times 20cm\] is rolled along its length to form a cylinder. Find the radius and volume of the cylinder.

Answer 1

Hint: The cylinder is a three-dimensional shape with two round shapes at either end and has two parallel lines connecting the round ends. These two round shapes are the base of the cylinder and their centers are joined by a line segment.
The volume of a 3-dimensional shape determines the capacity it can hold or the capacity it has, and in the case of a cylinder, it determines the capacity of the cylinder. The volume of the cylinder is given as \[V = \pi {r^2}h\] where, (r) is the radius of the base.

Complete step-by-step answer:
In this question, we need to determine the radius and the volume of the cylinder which is made from the rectangular sheet. For this we need to use the properties of the rectangles and the cylinder.
Given the rectangular dimension sheet of paper

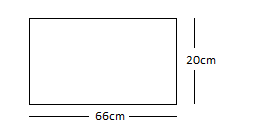
Length \[l = 66cm\]
Breadth \[b = 20cm\]
Since the rectangular sheet is rolled along its length, the width of the rectangle becomes the height of the cylinder

\[h = b = 20cm\]
And the length of the rectangular sheet becomes the circumference of the cylinder where the circumference of the cylinder is given as\[2\pi r\], hence
\[
  2\pi r = l \\
  r = \dfrac{l}{{2\pi }} \\
   = \dfrac{{66}}{{2 \times \dfrac{{22}}{7}}} \\
   = \dfrac{{21}}{2} \\
   = 10.5cm \\
 \]

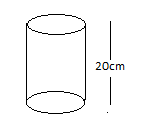
Hence the radius of the cylinder formed will be \[r = 10.5cm\], and the height will be \[h = 20cm\]
The volume of the cylinder is given as \[V = \pi {r^2}h\]
Now substitute the values in the formula
\[
  V = \pi {r^2}h \\
  V = \pi \times {\left( {10.5} \right)^2} \times 20 \\
   = \left( {\dfrac{{22}}{7}} \right) \times 10.5 \times 10.5 \times 20 \\
   = 6929.99 \\
   \simeq 6930c{m^3} \\
 \]
Hence the volume of the cylinder will be \[ = 6930c{m^3}\]

Note: To find the capacity of a closed curve/body, the volume is calculated for a three-dimensional object, and the area is calculated for a two-dimensional figure. It is interesting to note here that every three-dimensional body is originated by rotating/revolving the two-dimensional body.