Question

A rectangular sheet of metal, $xcm$ by $ycm$, has a square of side $zcm$ cut from each corner. The sheet is then bent to form a tray of depth $zcm$. Then find out the volume of the tray in cubic centimetres is
A.$z\left( {x - z} \right)\left( {y - z} \right)$
B.$xyz$
C.$z\left( {x - 2z} \right)\left( {y - 2z} \right)$
D.$\left( {x + y} \right)z$

Answer 1

Hint:As per the given data, firstly draw the diagram of the rectangle with the given measurements. Later on, cut the squares from the corners and form the tray as mentioned. Now imagine the dimensions of the tray which looks like a cuboid. Now the volume of cuboid will be equal to the volume of the tray.

Complete step-by-step answer:
It is given that there is a rectangular sheet with dimensions $xcm$ and $ycm$.
Let us consider $xcm$ as the length of the rectangle and $ycm$ as the breadth of the rectangle.
As per the data mentioned, now cut the square with side length $zcm$ from each corner of the rectangle.
It will then look as the following diagram.

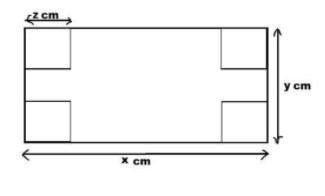
When you remove those small squares and convert it in the form of cuboid,
The dimensions will change as follows:

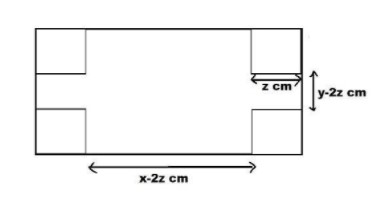
The length of the cuboid will be $\left( {x - 2z} \right)cm$ as we are removing the squares from both left and right sides of the rectangle.
Similarly,
The width of the cuboid will be $\left( {y - 2z} \right)cm$ as we are removing the squares from both top and bottom sides of the rectangle.
At last the height of the cuboid will be the $zcm$.
Since we have all the dimensions of the cuboid and already, we are great familiar with the formula of volume of cuboid.
Volume of the cuboid with $l$ length, $b$ width and $h$ height is $lbh$
Substituting the values of length, width and height, we get
Volume of the tray $ = \left( {x - 2z} \right)\left( {y - 2z} \right)z$ in cubic centimetres.

So, the correct answer is “Option C”.

Note:Remember one thing that when you get any this kind of problems, you must draw the diagram according to the given information and later on imagination is the only tool. To be perfect, explore different kinds of structures and their dimensions and in case you find it difficult to imagine, try it in the real world with paper.