Question

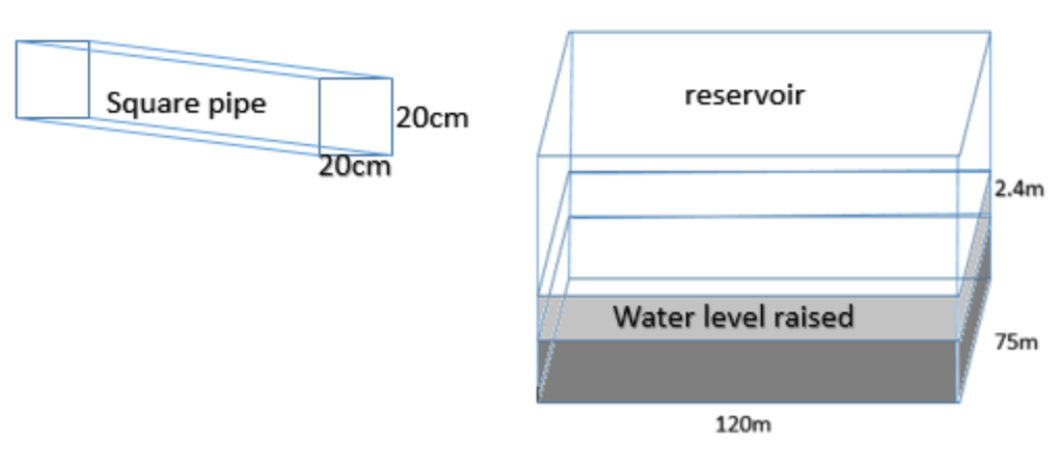
A rectangular reservoir is 120m long and 75m wide. At what speed per hour must water flow into it through a squared pipe of 20cm wide so that the water rises by 2.4m in 18 hours

Answer 1

Hint: Since we know that the water in the reservoir rises by 2.4m and we know the length and width of the reservoir we can find the volume of water risen in 18 hours. Now, this Volume is the same as the total volume of water that has flown through the pipe in 18 hours. Now we assume that speed of water is x. then use speed × time = distance to find the length of the squared pipe, hence find the volume of water flown from the squared pipe

Complete step-by-step solution:

Now first consider the water flowing through pipe
We are given that the pipe is squared pipe with width 20 cm = 0.2m
Hence we can say that the width and height of the pipe is 0.2m
Now let us assume the speed of water is ‘x’ m per hour.
Now we know that speed × time is distance
Hence the distance travelled by water is 18x.
Now note the water flows in the squared pipe whose width and height are 0.2m
And the length of water that flows is 18x.
Hence the volume of water that flows through pipe is 18x × 0.2m × 0.2m.
This gives us the volume of water that flows through the pipe is 0.72x …………….. (1)
Now consider the reservoir
A rectangular reservoir is 120m long and 75m wide and in 18 hours it is risen by 2.4m
Hence the volume of water that fills in 18 hours will be
2.4 × 120 × 75 = 21600 sq m ……………………….. (2)
Now the water in reservoir is filled due to the water that has flown through the pipe.
Hence the water has flown through the pipe in 18 hours is the volume of water that fills in 18 hours
Hence from equation (1) and equation (2) we get
$\begin{align}
  & 0.72x=21600 \\
 & x=\dfrac{21600}{0.72} \\
 & x=30,000 \\
\end{align}$
Hence we get the speed of water is 30,000m per hour
Which is 30km per hour
Hence the speed of water is 30km per hour.

Note: While taking the volume make sure the units of all the quantities are same. Here the width of pipe is given in cm. hence convert it in m. similarly we have taken speed in units m per hour and then in the end we again convert it into km per hour.