Question

A rectangular plot of land with dimensions $7m\times 8m$, consists of a square garden planted with tulips and a concrete path surrounding garden. The area of the garden is $\dfrac{9}{14}$ of the area of the plot of land. Calculate the length of one side of the square garden.

Answer 1

Hint: Let us assume that the side of the square garden is ‘x’ m. So, by using the formula: $\text{Area of square} ={{a}^{2}}$, get the area of square. Also, we have the length and breadth of the rectangular plot as 7m and 8 m respectively. So, by using the formula: \[\text{Area of rectangle}=l\times b\], find the area of the plot.
It is also given that the area of the square garden is $\dfrac{9}{14}$ of the area of the rectangular plot. So, get an equation in terms of x, and solve for x.

Complete step-by-step solution:

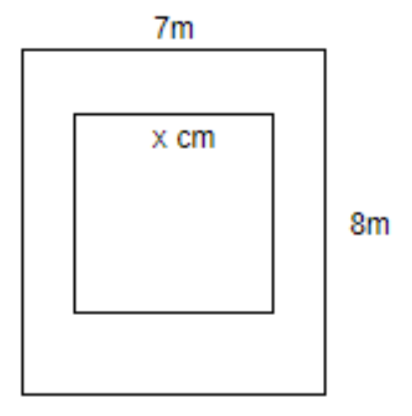
As we have assumed that, the side of the square garden is ‘x’ m.
So, by using the formula: $\text{Area of square}={{a}^{2}}$
We get:
The area of a square garden is: ${{x}^{2}}{{m}^{2}}................(1)$
Also, we have:
Length of rectangular plot = 7 m
The breadth of rectangular plot = 8 m
So, by using the formula: \[\text{Area of rectangle}=l\times b\]
We have:
The area of the rectangular plot is: $56{{m}^{2}}........................(2)$
Since it is mentioned that:
The area of the square garden is $\dfrac{9}{14}$ of the area of the rectangular plot.
So, we get a relation between equation (1) and (2) as:
\[\begin{align}
  & \Rightarrow {{x}^{2}}=\dfrac{9}{14}\times 56 \\
 & \Rightarrow {{x}^{2}}=9\times 4 \\
 & \Rightarrow {{x}^{2}}=36 \\
 & \Rightarrow x=6m \\
\end{align}\]
When we calculate the size of the square garden, we also get a negative value of x, i.e. - 6. Since the distance cannot be negative, we neglect the negative value. Therefore, x = 6 m.
Hence, the side of the square garden is 6 m.

Note: The students must read the question very carefully. Here, they must note that the area of the square garden is $\dfrac{9}{14}$ of the area of the rectangular plot and not vice versa. If they make a mistake in understanding this data, they will form the wrong equation and the value of x will also be different.