Question

A rectangular piece of paper measuring \[11\;cm \times 4\;cm\] is folded without overlapping to make a cylinder of height \[4\;cm\] . Find the volume of the cylinder.

Answer 1

Hint: Consider the example, take a Bisleri packaged drinking \[1\] litre water bottle. It would be wrapped around in the middle by a plastic sheet. Observe that the middle of that bottle is in the form of a cylinder which hints that the sheet wrapped around also takes the form of a cylinder. Then, on removing the wrapped sheet without breakage we can observe that the sheet is the form of a rectangle.
The reverse observation of the above example is the question we have. Then, the length of the rectangle will become the circumference of the base circle of the thus formed right-circular cylinder which can lead us in finding the radius of the cylinder.

Complete step-by-step answer:
Given that the height of the cylinder is \[4\;cm\] . So, when we fold the paper (like wrapping around) without overlapping with height as \[4\;cm\] we arrive at a right-circular cylinder with base circumference as \[11\;cm\] .
Observe that both open mouths of a right-circular cylinder are in the form of a circle. In this case, the circumference of those circles is \[11\;cm\] .
We know that the formula for circumference of a circle is \[2\pi R\] where \[R\] is the radius of the circle.

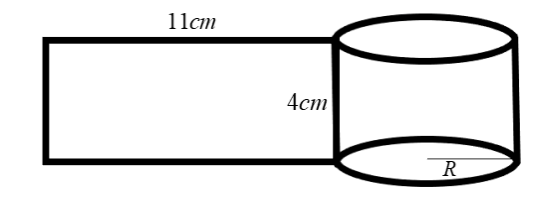
In this case, \[2\pi R = 11 \Rightarrow R = \dfrac{{11}}{{2\pi }} = \dfrac{{11}}{2} \times \dfrac{7}{{22}} = \dfrac{7}{4} = 1.75\]
Therefore, \[R = 1.75\;cm\] , the radius of the base circles of the right-circular cylinder so formed.
The formula for the volume of a right-circular cylinder is \[\pi {R^2}H\] cubic units.
In this case, consider \[H = 4\;cm\] .
Therefore, the volume of the given right-circular cylinder \[ = {\left( {1.75} \right)^2} \times 4\pi = 3.0625 \times 4\pi = 12.25\pi \simeq 12.25 \times \dfrac{{22}}{7} = 38.5\;c{m^3}\]
Thus, we obtained the volume of the right-circular cylinder to be \[38.5\;c{m^3}\] approximately.
So, the correct answer is “\[38.5\;c{m^3}\] ”.

Note: Here we considered the value of \[\pi \] to be \[\dfrac{{22}}{7}\] . We shall also consider the value of \[\pi \] to be \[3.14\] which is an approximate value. Since \[\pi \] is an irrational number it’s exact value can never be calculated. So, we have only arrived at an approximate solution to the given problem.