Question

A rectangular piece of cardboard is \[40\] inches wide and \[50\] inches long. Square \[5\] inches on a side are cut out of each corner, and the remaining flaps are bent up to form an open box. The number of cubic inches in the box is
F. \[1200\]
G. \[7875\]
H. \[6000\]
I. \[8000\]
J. \[10000\]

Answer 1

Hint:While solving the question one must remember that the cut of \[5\] in. is done on both the sides of the length of the box as a rectangle has two lengths similarly, the cut is also done in the width as well leaving a total cut size of \[5+5=10\] in. and apart from the sides a bottom bend is also made for the box to be closed at the bottom giving a height of \[5\] in. making the volume of the box as:
Volume\[=\text{Length}\times \text{Breadth}\times \text{Height}\]

Complete step by step solution:
According to the question given, the length, width and the height of the box is given as \[40\] in. wide and \[50\] in long, now the box is being folded up by \[5\] in. on all sides changing the rectangle base dimension of the box by \[5\] in. on all sides giving the base of the box new dimensions of:
The width of the box is \[40\] in. and the sides folded are on both sides making the width of the base of the box as:
\[\Rightarrow \left( 40-\left( 5+5 \right) \right)=30\] in.
The length of the box is \[50\] in. and the sides folded are on both sides making the length of the base of the box as:
\[\Rightarrow \left( 50-\left( 5+5 \right) \right)=40\] in.

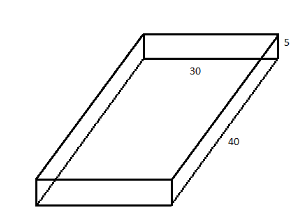
Now according to the diagram of the box, we have the dimensions of the box as width \[30\] in., length\[40\] in. and height as \[5\] in. Now using these dimensions, we find the volume of the box as:
Volume\[=\text{Length}\times \text{Breadth}\times \text{Height}\]
Volume\[=\text{40}\times \text{30}\times \text{5}\]
Volume\[=6000\] cubic in.
Therefore, the volume of the open box is \[6000\] cubic in.

Note: The dimensions are subtracted twice because the box is folded 2 times in the length section and 2 times in the width section but the height will remain \[5\] in. only thereby subtracting twice from both the length and the width.