Question

A rectangular piece is $20m$ long and $15m$ wide. From its four corners, quadrants of radii $3.5m$ have been cut. Find the area of the remaining part.

Answer 1

Hint: Here, we are given a rectangular piece which is $20m$ long and $15m$ wide. From its four corners, quadrants of radii $3.5m$ have been cut and we have to find the area of the remaining part. So firstly, we will find the area of a rectangle. After this, we will find the area of quadrants and in the end we will subtract the area of four quadrants from the area of the rectangle to get the area of the remaining part.
Formulae used:
Area of rectangle = length × breadth
Area of quadrant = $\dfrac{\theta }{{360^\circ }} \times \pi {r^2}$

Complete step-by-step solution:
Let us first draw the figure for the given question with the help of the information provided in the question.

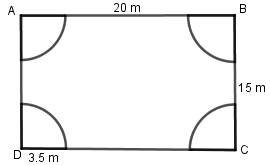
For area of rectangle:
Area of rectangle ABCD = length × breadth
Here length = $20m$, breath = $15m$
$ \Rightarrow Area = 20m \times 15m$
$ \Rightarrow Area = \left( {20 \times 15} \right){m^2}$
On multiplication, we get
$ \Rightarrow Area = 300{m^2}$
Area of rectangle = $300{m^2}$
For area of quadrant:
Area of quadrant = $\dfrac{\theta }{{360^\circ }} \times \pi {r^2}$
Radius of quadrant is $3.5m$ and $\theta = 90^\circ $ (As we know each interior angle of rectangle is $90^\circ $ and quadrant lies at the corner of rectangle between the two sides of rectangle, therefore $\theta = 90^\circ $).
Substitute the value of radius and $\theta $ in the above written formula.
 $ \Rightarrow Area = \dfrac{{90^\circ }}{{360^\circ }} \times \dfrac{{22}}{7} \times {\left( {3.5} \right)^2}{m^2}$
On cancelling, we get
$ \Rightarrow Area = \dfrac{1}{4} \times \dfrac{{22}}{7} \times {\left( {3.5} \right)^2}{m^2}$
$ \Rightarrow Area = \dfrac{1}{4} \times \dfrac{{22}}{7} \times 3.5 \times 3.5{m^2}$
On simplifying, we get
$ \Rightarrow Area = \dfrac{{22}}{{28}} \times 12.25{m^2}$
On solving, we get
$ \Rightarrow Area = 9.625{m^2}$
Area of one quadrant = $9.625{m^2}$
Area of four quadrants = $4 \times 9.625{m^2}$
$ = 38.5{m^2}$
Area of remaining part = Area of the rectangle – Area of four quadrants.
Area part of remaining = $\left( {300 - 38.5} \right){m^2}$
Area part of remaining = $261.5{m^2}$.

Note: A quadrant is one-fourth of a circle. When a circle is evenly divided into four sections by two perpendicular lines, each of the four areas is a quadrant. We can find the area of quadrants in the given question by another method also. As we know four quadrants make one circle. Therefore we can find the area of the circle instead of the area of four quadrants.
Area of circle = $\pi {r^2}$
$ \Rightarrow Area = \dfrac{{22}}{7} \times {\left( {3.5} \right)^2}{m^2}$
$ \Rightarrow Area = \dfrac{{22}}{7} \times 12.25{m^2}$
$ \Rightarrow Area = 38.5{m^2}$