Question

A rectangular paper of dimension 6 cm and 3 cm is rolled to form a cylinder with height equal to the width of the paper, then its base radius is?
A.$\dfrac{6}{\pi }cm$
B.$\dfrac{3}{{2\pi }}cm$
C.$\dfrac{6}{{2\pi }}cm$
D.$\dfrac{9}{{2\pi }}cm$

Answer 1

Hint:
A cylinder is a three-dimensional solid that holds two parallel bases joined by a curved surface, at a fixed distance. These bases are normally circular in shape and the centers of the two bases are joined by a line segment. A right circular cylinder has a circular base and top. So, in order to make a rectangular paper in the form of a cylinder, we have to roll the length of the rectangular paper.
The length of the rectangular phase is equal to the circumference of the circle which forms the base of the cylinder. And the width of the paper becomes the height of the cylinder.
Circumference of the circle = $2\pi r$

Complete step by step solution:

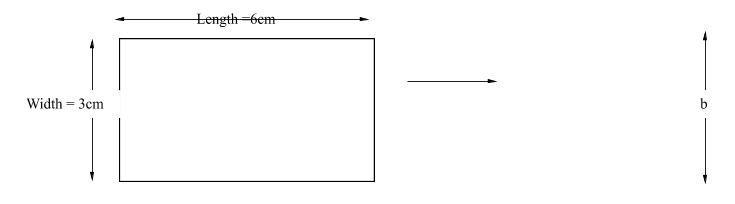
In order to make a cylinder from a rectangular paper, we have to roll its length as shown in figure. In this case the length of rectangular paper is equal to the circumference of the base of the cylinder.
∴ Let the width of rectangular paper = b = 3 cm
Length of rectangular paper = l = 6 cm
Radius of base of cylinder = r
From the diagram,
Length of rectangular paper = circumference of base of cylinder
$l = 2\pi r$
Hence, the radius of the base of the cylinder is $\dfrac{6}{{2\pi }}cm$ .
∴ Option (C) is correct.

Note:
. Students must remember that or understand that the base of the cylinder is circular. During rolling rectangular paper the length of rectangular paper is equal to circumference of base of cylinder. Students must know the formula of circumference of circle i.e.$2\pi r$, where r is the radius.