Question

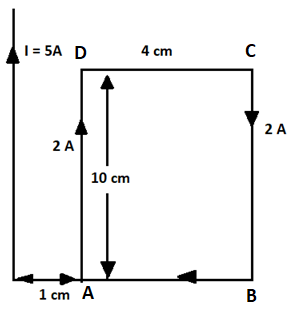
A rectangular loop of wire of size $4cm \times 10cm$ carries a steady current of $2A$. A straight long wire carrying $5A$ current is kept near the loop as shown. If the loop and the wire are coplanar, find:

(i) the torque acting on the loop and
(ii) the magnitude and the direction of the force on the loop due to the current carrying wire.

Answer 1

Hint: For first case, recall all the concepts related to torque and the formula for the torque on the current carrying conductor. Then for the second case, recall the formula for finding the force due to the current carrying wire. For finding the direction remember the right-hand thumb rule.

Formula used:
$\vec \tau = \vec M \times \vec B$
Where, $\vec B$ is the magnetic field current loop experiences
$\vec M$ is the magnetic moment of a current loop given by,
$M = IA$, $I$ is the current flowing in the current loop and $A$ is the area of the loop.
The magnetic force due to straight wire is given by,
$F = i\vec l \times \vec B$
Where, $i$ is the current flowing,
$l$ is the length of the current loop
$\vec B$ is the magnetic field that current loop experiences

Complete step by step solution:
(i) We know that, torque on the current carrying conductor is given by,
$\vec \tau = \vec M \times \vec B$
Here, in this case the magnetic moment and the magnetic field have the same direction. Therefore,
$\theta = {0^ \circ }$
On further solving the cross product the torque becomes,
$ \Rightarrow \tau = MB\sin \theta $
As $\theta = {0^ \circ }$, we get torque is equal to zero
$\tau = 0$

Therefore, the torque acting on the loop is $\tau = 0.$

(ii) On line AB and CD magnetic forces due to the straight wire are equal and opposite. So they cancel out each other.
So, there are only two magnetic forces acting on line AD and CB.
We know, the magnetic force due to straight wire is given by,
$F = i\vec l \times \vec B$
$ \Rightarrow F = ilB$ {here given both loop and wire coplanar}
Where, $i$ is the current flowing,
$l$ is the length of the current loop
$\vec B$ is the magnetic field that current loop experiences
We know that,
$B = \dfrac{{{\mu _0}I}}{{2\pi r}}$
Now the Magnetic force on segment AD is given by,
${F_{AD}} = \dfrac{{{\mu _0}iIl}}{{2\pi {r_1}}}$ (towards left)
Similarly, the Magnetic force on segment CB is given by,
${F_{CB}} = \dfrac{{{\mu _0}iIl}}{{2\pi {r_2}}}$ (towards right)
So, the net force on the loop due to the current carrying wire is,
${F_{net}} = {F_{AD}} - {F_{CB}}$
$ \Rightarrow {F_{net}} = \dfrac{{{\mu _0}iIl}}{{2\pi }}\left( {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right)$
We have given in the question,
$i = 5A$,
$I = 2A$,
${r_1} = 1cm = {10^{ - 2}}m$,
$l = 10cm = {10^{ - 1}}m$ and
${r_2} = 1cm + 4cm = 5cm$
$ \Rightarrow {r_2} = 5 \times {10^{ - 2}}$
On putting all the values in the above formula, we get
$ \Rightarrow {F_{net}} = 2 \times {10^{ - 7}} \times 2 \times 5 \times {10^{ - 1}}\left( {\dfrac{1}{{{{10}^{ - 2}}}} - \dfrac{1}{{5 \times {{10}^{ - 2}}}}} \right)$
$ \Rightarrow {F_{net}} = \dfrac{{20 \times {{10}^{ - 8}}}}{{{{10}^{ - 2}}}}\left( {1 - \dfrac{1}{5}} \right)$
On further solving, we get the value of the net force on the loop due to the current carrying wire is,
$ \Rightarrow {F_{net}} = 1.6 \times {10^{ - 5}}N$
The force is attracted in nature and towards the conductor.

Therefore, the magnitude and the direction of the force on the loop due to the current carrying wire is ${F_{net}} = 1.6 \times {10^{ - 5}}N$, and the direction of force towards the conductor.

Note: The magnetic moment of a current loop can be defined as the product of the current flowing in the loop and the area of the rectangular loop and the torque exerted on a current-carrying coil placed in a magnetic field can be given by the vector product of the magnetic moment and the magnetic field.