Question

A rectangular loop has a sliding connector PQ of length l and resistance $R\Omega $ and it is moving with a speed v as shown. This set-up is placed in a uniform magnetic field going into the plane of paper. The three currents ${{I}_{1}},{{I}_{2}}$ and I are

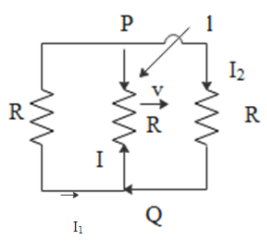
Answer 1

Hint: A moving conductor is equivalent to a battery of emf equal to the motional emf. To find ${{I}_{1}},{{I}_{2}}$ and apply Kirchoff’s law we will get two equations. By adding and solving them we will get the value of ${{I}_{1}},{{I}_{2}}$ and I. While applying Kirchoff’s voltage law the algebraic sum means to take into account the polarities and signs of the sources and voltage drop around the loop. We know that flow of current is from positive to negative.
Formula used:
Motional emf,
E=vBl
Where, E is the motional emf
v is the voltage across R
B is the magnetic field
l is the length of sliding connector

Complete answer:

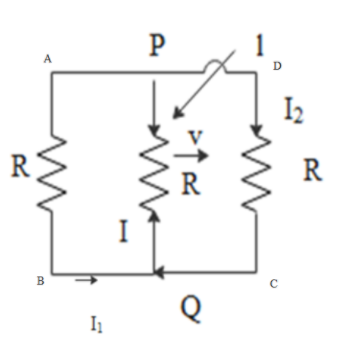
Applying Kirchoff’s voltage law along ABQP and along DCQP we get,
$\begin{align}
  & {{I}_{1}}R+IR-vBl=0............(1) \\
 & {{I}_{2}}R+IR-vBl=0.............(2) \\
\end{align}$
Adding equation (1) and (2).
$\Rightarrow $ $({{I}_{1}}+{{I}_{2}})R+2IR=2vBI$ ……….(3)
From equivalent circuit,
$\Rightarrow $ $I={{I}_{1}}+{{I}_{2}}$ ……………..(4)
Applying equation(4) in equation(3),
$\begin{align}
  & 2IR+IR=2vBl \\
 & 3IR=2vBl \\
\end{align}$
Then,
$\Rightarrow $ $I=\dfrac{2vBl}{3R}$
From equation (4) we get,
Here ${{I}_{1}}={{I}_{2}}=\dfrac{I}{2}$
Thus,
$\Rightarrow $ ${{I}_{1}}={{I}_{2}}=\dfrac{vBl}{3R}$

Additional information:
Kirchoff’s voltage law states that the algebraic sum of the potential difference in any loop must be equal to zero. This is because a closed circuit is a closed conducting path so no energy is lost. That is the conservation of energy in a closed path. Current entering a junction will be positive and current leaving the junction will be negative.
Kirchhoff's Voltage Law (KVL) is Kirchhoff's second law that deals with the conservation of energy around a loop path. The voltage law states that for a closed-loop system series path the algebraic sum of all the voltages around any closed-loop system during a circuit is adequate to zero.
For KCL, incoming currents are always said to be positive and outgoing currents are negative at a node/junction.
For KVL, while considering a loop/mesh, there is a potential rise when moving from negative to positive terminal of a battery and moving against the direction of current through a resistor. Potential drops in vice-versa situation.

Note:
While applying Kirchoff’s voltage law the algebraic sum means to take into account the polarities and signs of the sources and voltage drop around the loop. We know that flow of current is from positive to negative. Thus as we are travelling in the direction of current flow, there will be a fall in potential.