Question

A rectangular loop carrying a current i is situated near a long straight wire such that the wire is parallel to one of the sides of the loop is in the pane of the loop. If steady current I is established in the wire as shown in fig. the loop will

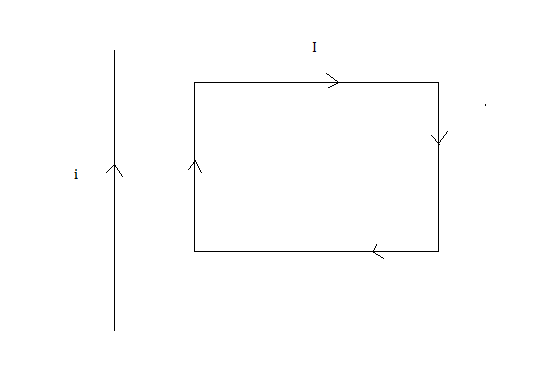
A. rotate about an axis parallel to the wire
B. move away from the wire
C. move towards the wire
D. remain stationary

Answer 1

Hint: The movement of the current carrying rectangular loop in presence of the current carrying long straight wire depends on the direction of current and the force of attraction and repulsion accordingly.

Formula used:
The force F on a wire due to the another wire is given by,
\[F=\dfrac{{{\mu }_{0}}}{2\pi }\dfrac{{{I}_{1}}{{I}_{2}}}{r}L\]
Where \[{{I}_{1}}\]is the current in the first wire, \[{{I}_{2}}\] is the current in the second wire and L is the length of the wire on which force is acting due to another wire( having current \[{{I}_{1}}\]), and r implies the distance between two parallel wires.

Complete step by step solution:
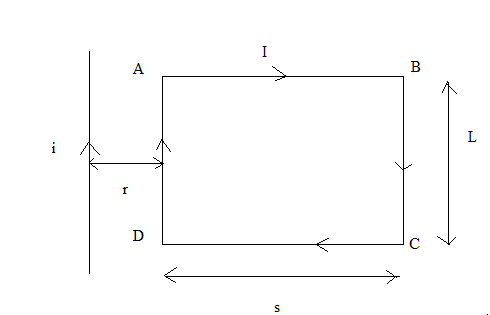
In the figure below, assuming r as the distance between the long straight wire, carrying current i , and the rectangular loop, carrying current I. Let s be the breadth of the rectangular loop and L be the length of the rectangular loop.

Generally, for a wire of length L carrying current I , placed in a uniform magnetic field \[\overrightarrow{B}\], the magnetic field force F is given by
\[F=BIL\sin \theta \]
From the above figure, the vertical portion of the rectangular loop i.e., AD and BC contribute to the force, because for the horizontal part i.e., AB and DC the forces will cancel out.
So, FAD (attractive force) \[=\dfrac{{{\mu }_{0}}}{2\pi }\dfrac{{{I}_{i}}}{r}L\] , and
    FBC (repulsive force) =\[\dfrac{{{\mu }_{0}}}{2\pi }\dfrac{{{I}_{i}}}{r+s}L\]
Where, r is the distance from the long straight wire to AD and s is the breadth of the wire.
Clearly, FAD > FBC

Therefore, the loop will come closer to the wire.

Therefore, option C is the correct answer.

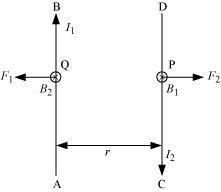
Additional information: There are two cases for two parallel current carrying conductors: -
Case-1: when the two parallel-placed conductors carry current in same directions an attractive force is created between the two conductors hence, they tend to move towards each other.

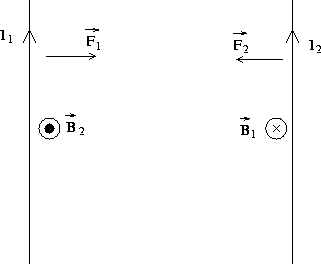
Case-2: when the two parallel-placed conductors, carry current in opposite directions, a repulsive force is created between the two conductors hence, they tend to move away from each other as shown in the figure below:

Note: The force is directed towards the straight wire, as the current in the rectangular loop is in the same direction (AD) as in the straight wire.