Question

A rectangular grassy plot is \[112\] m long and \[78\] m broad. It has a gravel path \[2.5\] m wide all around it on the side. Find the area of the path and the cost of constructing it at its \[4.50\] per square meter. Find the sum of the values.

Answer 1

Hint: To find the area of the gravel path, find the area of the inner rectangular field and the total area of the field. Then subtract the area of the inner rectangular field from the total area to get the area of the gravel path. Then multiply the area of the gravel path with Rs \[4.50\] to find the total cost.

Complete step-by-step solution:
It is given to us that the length of a rectangular grassy plot is \[112\] m and the width of a rectangular grassy plot is \[78\] m. It is also given that it has a gravel path of width \[2.5\] m around it on the sides. For better understanding, you should know that gravel consists of very small stones. It is often used to make paths. To get a rough idea to solve the question further see the below diagram.

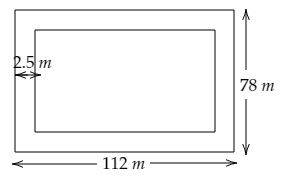
According to the question we have to find the area of the path. So we have to find two types of areas. First we will find the total area of the rectangle which has length as \[112\] m and breadth as \[78\] m .Then we will find the area of the inner rectangle as shown in the diagram.
In this case, to find total area we use the formula,
Total area = Length of the outer rectangle \[ \times \] Breadth of the outer rectangle
And to find the inner area we simply use the formula of rectangle that is
Area \[ = \] Length of the inner rectangle \[ \times \] Breadth of the inner rectangle
So let’s first find the length and breadth of the inner rectangle.
Length of the inner rectangular field \[ = \] Length of the outer rectangle \[ - \] (\[2\]\[ \times \] width of the path)
It is given to us that length of the outer rectangle is \[112\] m and the given width of the path is \[2.5\] m .Therefore the length of inner rectangular field will be
Length of the inner rectangular field \[ = \] \[112 - \left( {2 \times 2.5} \right)\] i.e.,
Length of the inner rectangular field \[ = \] \[107\] m
Similarly, the breadth of the inner rectangle \[ = \] \[78 - \left( {2 \times 2.5} \right)\]
i.e., The breadth of the inner rectangle \[ = \] \[73\] m
Therefore, the area of the inner rectangular field \[ = \] \[107 \times 73\]
\[= 7811\] \[{m^2}\]
Now we will find the area of the rectangle with sides \[112\] m and \[78\] m. Therefore,
Total area \[ = \] \[112 \times 78\]
\[ = 8736{\text{ }}{m^2}\]
Now, Area of the gravel path \[ = \] Total area \[ - \] area of the inner rectangular field
\[= 8736 - 7811\]
\[= 925{\text{ }}{m^2}\]
Now, the cost of constructing the path is Rs \[4.50\] per square meter.
Therefore, the cost of constructing the complete path \[ = 925 \times 4.50\]
\[ = Rs{\text{ }}4162.5\]
Thus, the total cost of constructing the path is \[Rs{\text{ }}4162.5\]

Note: Avoid silly mistakes during calculations. Keep in mind the formulas we used in the solution. Remember the steps in which we have found the values of the length and breadth of the inner rectangular fields. In these types of questions, first try to make the diagram, this will help you to answer the given question easily.